Exercice 1 tp

Calculer cosx et tanx sachant que

sinx =	-2	et x∈]	-π	;	π	]
	3		2		2

Correction

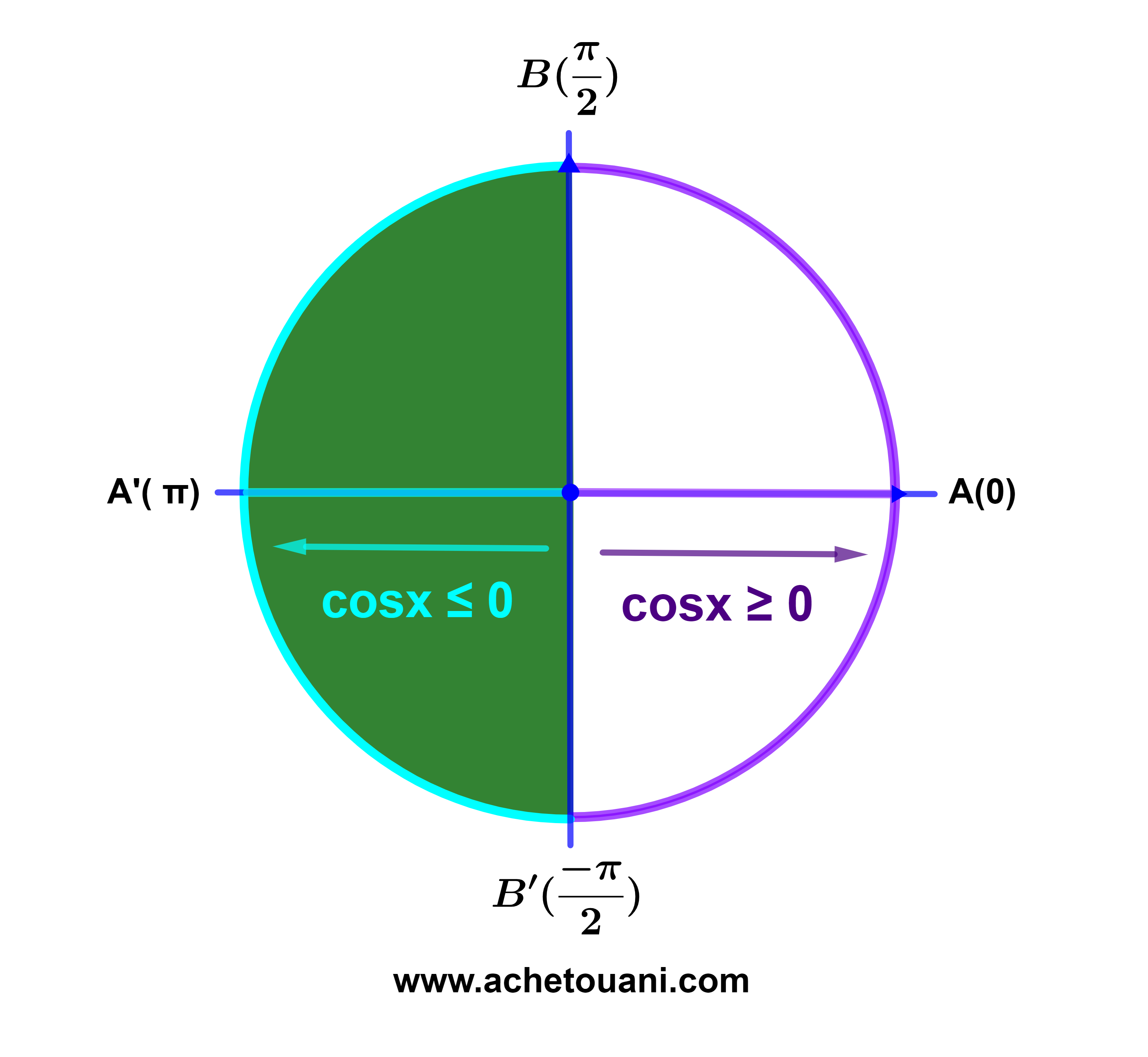
Rappel

Si x∈[	-π	;	π	] alors cosx≥0
	2		2

Si x∈[-π;	-π	] ∪ [	π	; π] alors cosx ≤0
	2		2

On a

x∈]	-π	;	π	]
	2		2

donc cosx≥0
ainsi cosx=√(1-sin²x).

cosx = √(1-(	-2	)²)
	3
= √(	9-4	)
	9
=	√(5)
	3

2) Puisque cosx≠0 alors tanx existe.

tanx =	sinx
	cosx

ainsi

tanx =	-√(5)
	2

Exercice 2 tp

Soit x∈]-π;0]
et

cos(x) =	2
	3

Calculer tan(x) puis sin(x).

Correction

cosx≠0 donc tanx existe.
On utilise la relation

1+tan²(x) =	1
	cos²x

donc

tan²(x) = -1+	1
	cos²x
tan²(x) = -1+(	3	)²
	2

Signifie

tan²(x) =	-4+9
	4
=	5
	4

On détermine le signe de tanx.
x∈]-π;0] donc il y'a deux cas.

Si x∈]-π;	-π	[
	2

alors cosx≤0 ce qui n'est pas car d'après les données cosx>0.

Si x∈]	-π	;0]
	2

alors cosx≥0 mais sinx≤0 donc tanx≤0 et par conséquent

tan(x) = -	√(5)
	2

Calcul de sinx.
sinx=cosx.tanx donc

sin(x) = -	√(5)
	3