Nombres complexes (7)
rappel
Soit z∈ℂ* tel que z = [r ; θ]
Les nombres r et θ sont appelés les coordonnées polaires du point M
en précisant le plan complexe rapporté à un repère orthonormé direct (O ; u→ ; v→) et on écrit M(r ; θ)
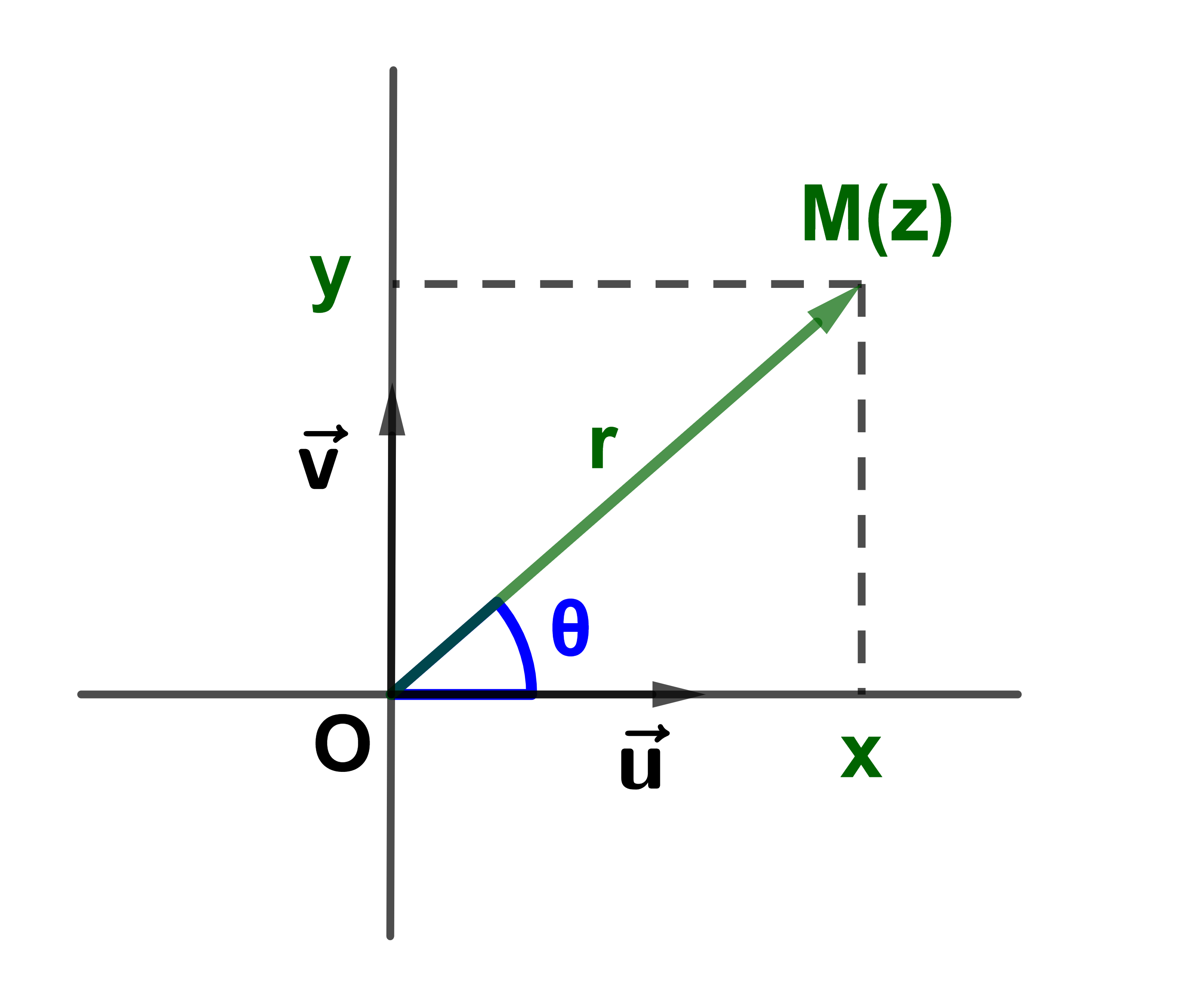
Les les coordonnées cartésiennes du point M dans un plan rapporté à un repère sont des nombres réels x et y
tels que x = rcosθ et y = rsinθ
Exercice 1 tp
Soit M un point défini par des coordonnées polaires
| M( 2 | ; | π | ) |
| 4 |
Déterminer les coordonnées cartésiennes du point M
Correction
On a
| x = 2cos | π | et | y = 2sin | π |
| 4 | 4 |
Ainsi les coordonnées cartésiennes du point M sont définie par le couple (√(2) ; √(2)) et on écrit également M(√(2) ; √(2)) en précisant le repère cartésien (O ; u→ ; v→)
Exercice 2 tp
Dans un plan rapporté à un repère
orthonormé direct (O ; u→ ; v→) , on considère un point M définie par
OM→ = u→ + √(3)v→
Déterminer les coordonnées polaires du point M.