تمرين 1 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) نعتبر مستقيمين
(D): x - 2y + 3 = 0 و (D'): 2x + y + 1 = 0
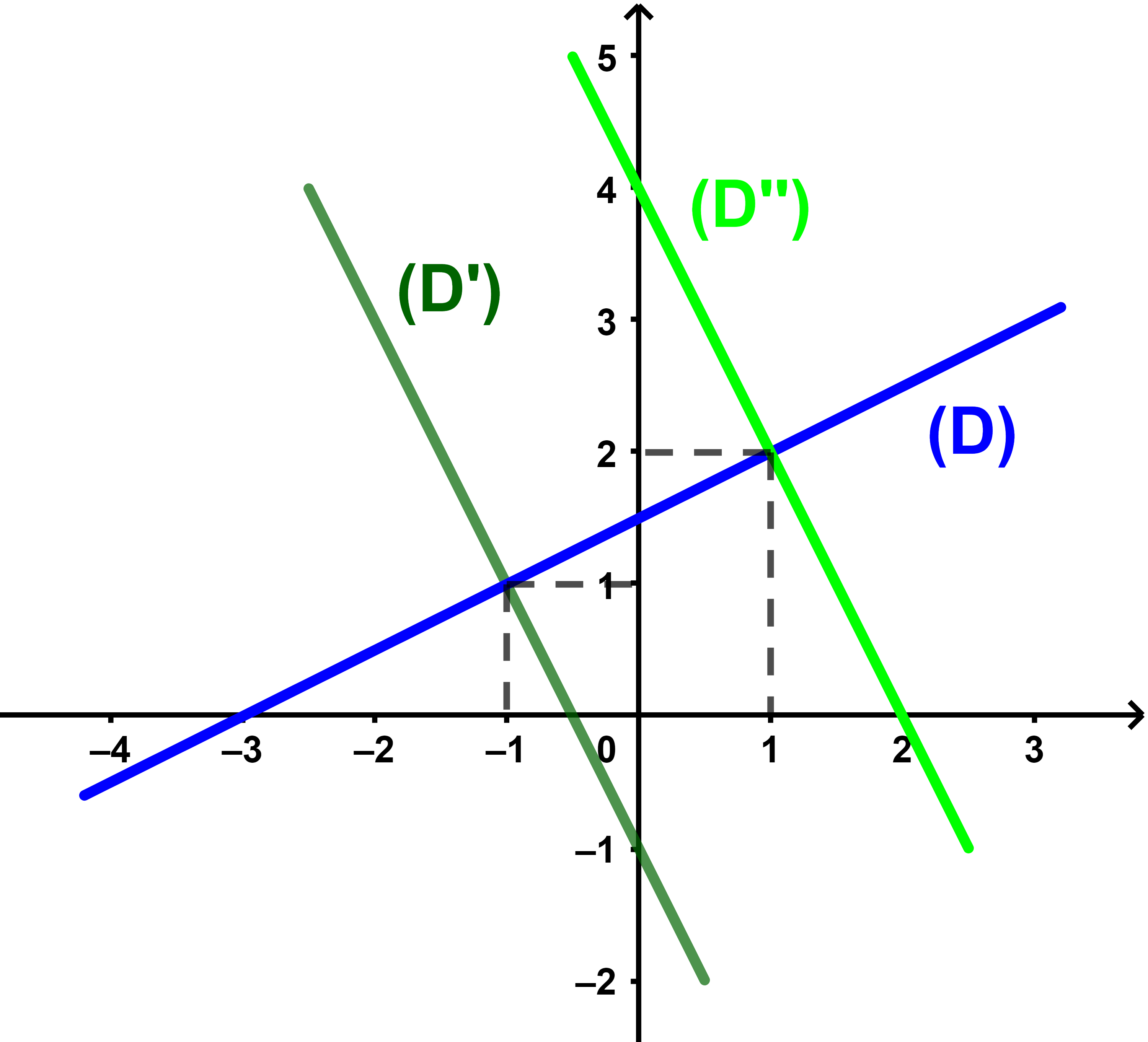
1) انشئ المستقيمين (D) و (D')
2) بين ان (D)⊥(D')
3) حدد نقطة تقاطع (D) و (D')
4) حدد معادلة للمستقيم (D") المار من النقطة E(2 ; 0) والعمودي على (D) ثم انشئه
5) ما هو الوضع النسبي للمستقيمين (D') و (D") ?

تصحيح

1) للتذكير لرسم مستقيم يكفي تحديد نقطتين منه لانه يمر منهما

x = -3	;	y = 0	→	A(-3 ; 0)∈(D)
x = 1	;	y = 2	→	B'(1 ; 2)∈(D)

اذن المستقيم (D) يمر من النقطتين A و B
اي (D) = (َAB)

x = 0	;	y = -1	→	A'(0 ; -1)∈(D')
x = -1	;	y = 1	→	B(-1 ; 1)∈(D')

والمستقيم (D') يمر من النقطتين A' و B'
اي (D') = (A'B')

2) نحدد ميل (D)
x - 2y + 3 = 0 يعني 2y = x + 3

y =	1	x +	3
	2		2

اذن

m =	1
	2

ميل (D) هو m = (0,5)

نحدد ميل (D')
2x+y+1=0 يعني y = -2x - 1
اذن m' = -2 ميل (D')
وبما ان m.m'=-1 فان (D)⊥(D')

3) لتحديد نقطة تقاطع المستقيمين يكفي حل النظمة التالية

{	y = -2x - 1
	x - 2y + 3 = 0

لذلك يمكن استعمال طريقة التعويض

{	y = -2x - 1
	x - 2(-2x - 1) + 3 = 0

يعني

{	y = -2x - 1
	5x = -5

اذن

{	y = - 2.	(-1)	- 1 = 1
	x =	- 5	= -1
		5

ومنه فان

{	y =	1
	x =	-1

وبالتالي (D) ∩ (D') = {E(-1 ; 1)}
4) (D)⊥(D") اذن m.m" = -1 أي m" = -2
ومنه فان معادلة (D")
تكتب على الشكل y = -2x + p"
وبما ان E∈(D") فان الزوج (2 ; 0) يحقق المعادلة
اذن 0 = -2.2 + p" أي p" = 4
وبالتالي (D"): y = -2x + 4
أي (D"): 2x + y - 4 = 0

5) لدينا (D)⊥(D') و (D)⊥(D")
اذن (D') || (D")
سؤال هل (D') و (D") متوازيان قطعا ?
لدينا A'(0 ; -1)∈(D') هل A'(0 ; -1)∈(D") ?
(D") : y = -2x + 4
-1 = -2.0 + 4 يعني -1 = 4 وهذا غير ممكن ومنه فان A'(0 ; -1)∉(D")
اذن (D') ≠ (D") وبالتالي فانهما متوازيان قطعا