تمرين 1 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→)
ادرس اشارة العدد x + y - 2
ثم حل مبيانيا المتراجحة
x + y - 2 < 0

تصحيح

(a) اشارة x+y-2
أولا ننشئ المستقيم (D) الذي معادلته x+y-2 = 0

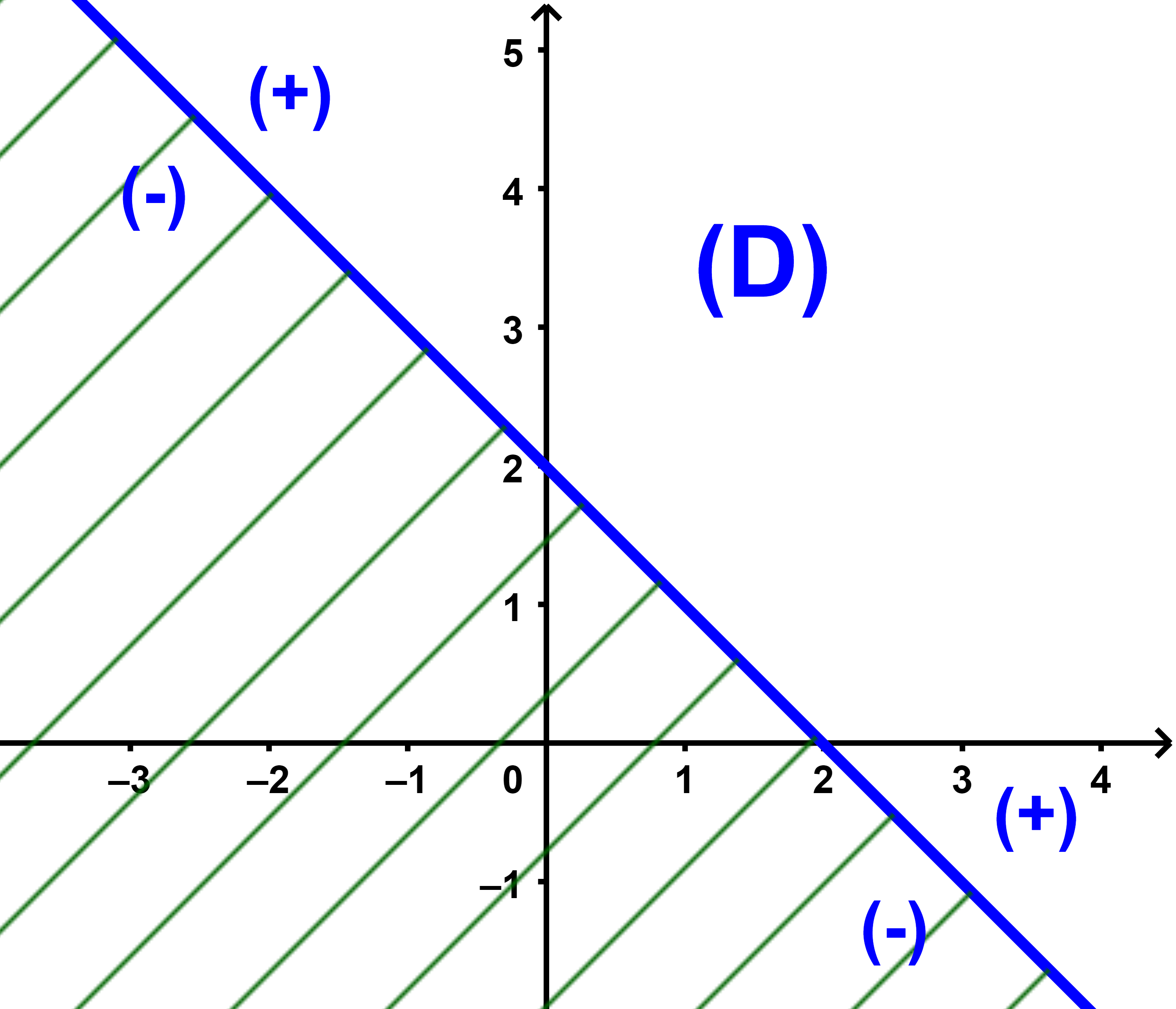ثانيا نعتبر نقطة لا تنتمي الى المستقيم (D) لتكن O(0;0)
لدينا 0+0- 2 = - 2 < 0 اذن نصف المستوى الذي حدوده (D) ويحتوي على النقطة O
معرف بالمتراجحة x+y-2 < 0

ونصف المستوى الذي حدوده (D) ولا يحتوي على النقطة O معرف بالمتراجحة x+y-2 > 0
(b) مجموعة حلول المتراجحة x+y-2 < 0 هي مجموعة ازواج احداثيات نقط نصف المستوى الذي حدوده (D) ويحتوي على النقطة O

تمرين 2 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→)
ادرس اشارة العدد x - y + 2
ثم حل مبيانيا المتراجحة
x - y + 2 > 0

تصحيح

(a) اشارة x-y+2
أولا ننشئ المستقيم (D') الذي معادلته x-y+2=0
ثانيا نعتبر نقطة لا تنتمي الى المستقيم (D')

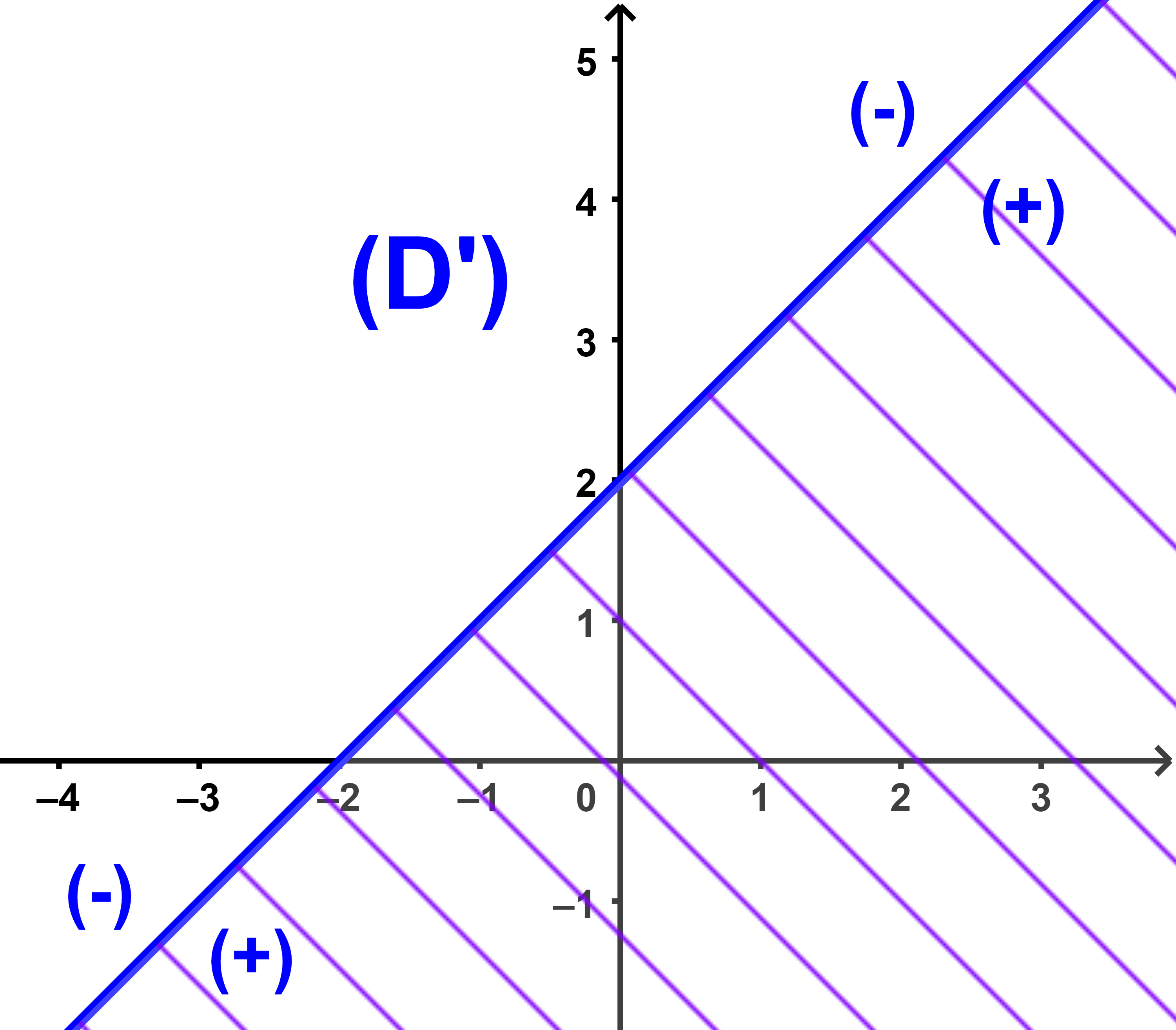
نعتبر النقطة O(0 ; 0)
لدينا 0-0+2 = 2 > 0
اذن نصف المستوى الذي حدوده (D') ويحتوي على النقطة O
معرف بالمتراجحة x-y+2 > 0
ونصف المستوى الذي حدوده (D') ولا يحتوي على النقطة O
معرف بالمتراجحة x-y+2 < 0

(b) مجموعة حلول المتراجحة x-y+2 < 0 هي مجموعة ازواج احداثيات نقط نصف المستوى الذي حدوده (D') ولا يحتوي على النقطة O

تمرين 3 tp

المستوى منسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) حل مبيانيا المتراجحة
(I): (x+y-2)(x-y+2) < 0
استنتج حلول النظمة

تصحيح

ينبغي انشاء المستقيميين (D): x + y - 2 = 0
و (D'): x - y +2 = 0 في نفس المعلم
(a) (I): (x+y-2)(x-y+2) < 0
تعني x+y-2 و x-y+2 لهما نفس الاشارة

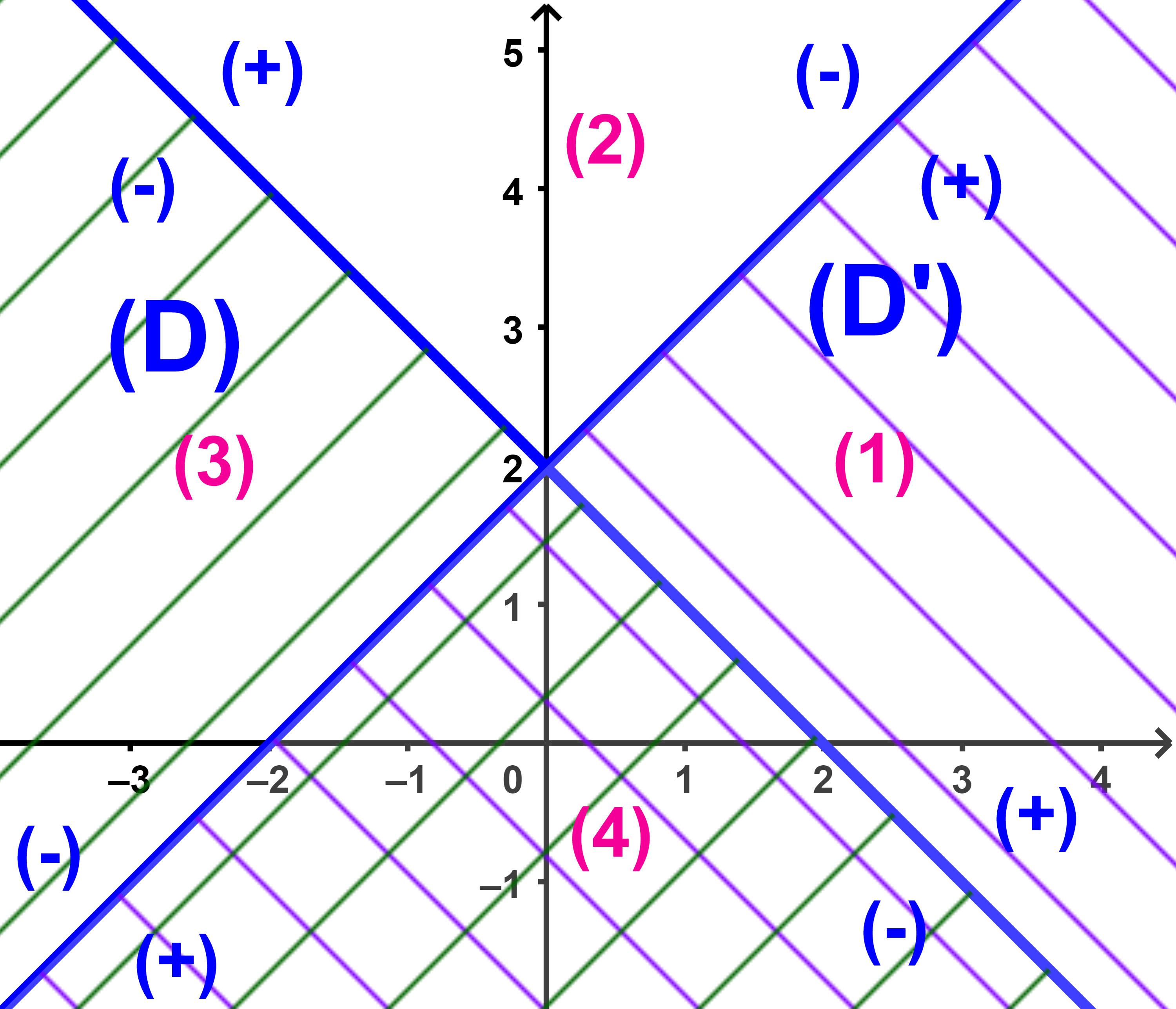
اذن مجموعة حلول المتراجحة (I) هي مجموعة ازواج احداثيات نقط الجزأين (1) و (3) من المستوى
(b) مجموعة حلول النظمة (S) هي مجموعة ازواج احداثيات نقط الجزأ (4) من المستوى.