Calcul de probabilités (8)
Exercice 1 tp
Une urne contient 3 boules bleues 5 boules rouges et 2 boules vertes, toutes les boules sont indiscernables au toucher. On tire au hasard trois boules successivement et avec remise
Calculer la probabilité de chacun des événements suivants
1) B: tirer trois boules bleues
2) R: Tirer trois boules rouges
3) V: Tirer trois boules vertes
4) E: tirer 1 boule bleue une boule rouge et 1 boule verte dans cet ordre
Correction
Dans cette expérience , le tirage successif et avec remise , il s'agit donc des arrangement avec répétition
cardΩ = 10³ = 1000
1) B: Tirer tois boules bleues
cardB = 3³ = 27
Donc
| p(B) = | 3³ | = | 27 |
| 10³ | 1000 |
2) R: Tirer trois boules rouges
cardR = 5³ = 125
| p(R) = | 5³ | = | 125 | = | 1 |
| 10³ | 1000 | 8 |
3) V: Tirer trois boules vertes
cardV = 2³ = 8
Donc
| p(V) = | 2³ | = | 8 | = | 1 | 10³ | 1000 | 125 |
4) E: tirer 1 boule bleue une boule rouge et 1 boule verte dans cet ordre
cardE = 3×5×2 = 30 donc
| p(E) = | 3×5×2 | = | 30 | = | 3 | 10³ | 1000 | 100 |
Exercice 2 tp
Le tableau ci-dessous détermine la loi de probabilité d'une variable aleatoire X
| xi | 0 | 1 | 2 | 3 | 4 | |
| p(X=xi) | 0,2 | 0,1 | 0,4 | 0,2 | 0,1 |
1) Déterminer F la fonction de la répartition de la variable aléatoire X.
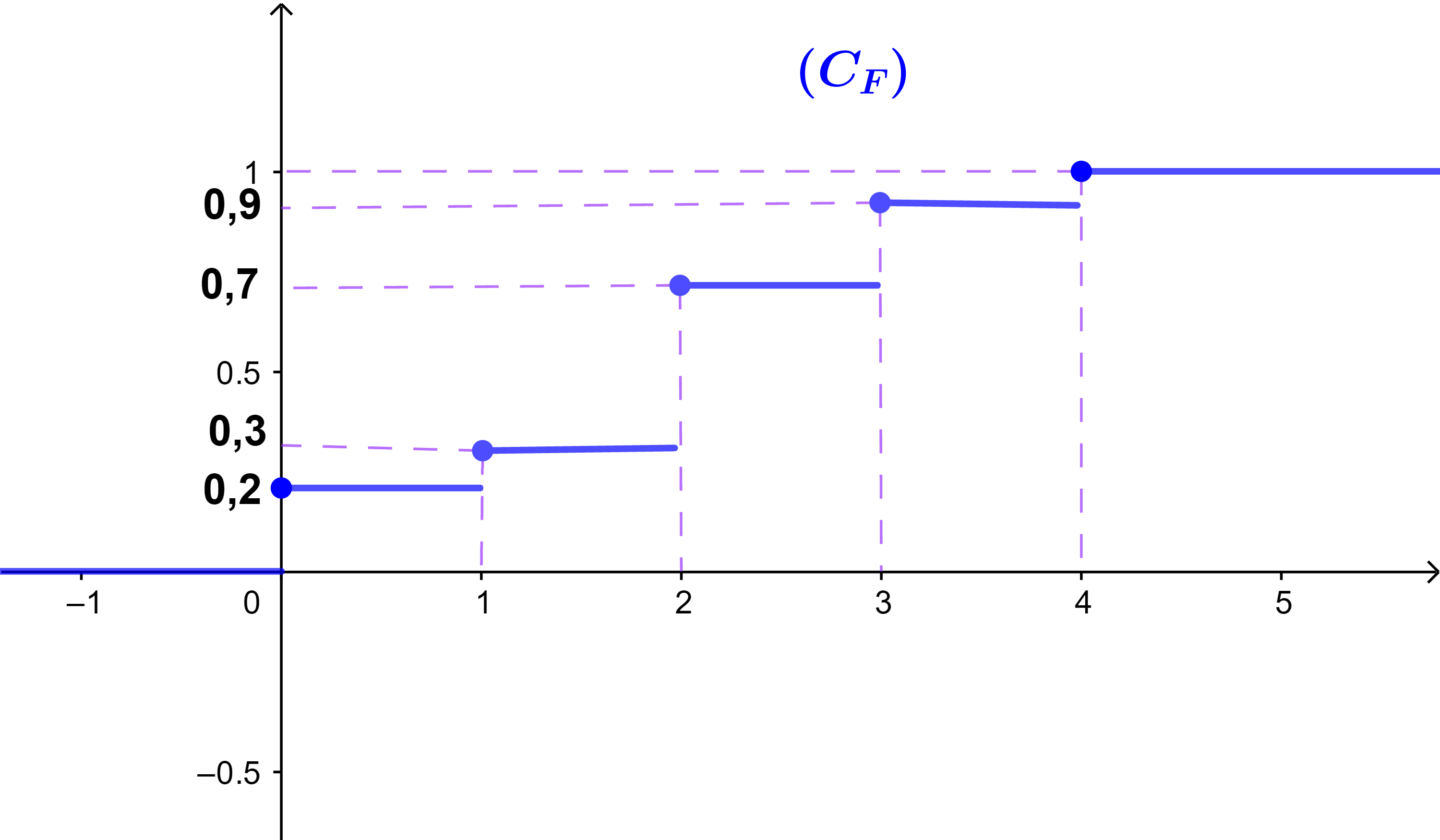
2) Tracer dans un repère orthogonal la courbe représentative de la fonction de répartition F
Correction
1) On rappelle que F est définie de IR vers [0;1] par
F(x) = p(X < x)
| X(Ω) = | {0 ; 1 ; 2 ; 3 ; 4} |
| Si x∈]-∞;0] | F(x)=0 |
| Si x∈]0;1] | F(x)=p(X=0)=0,2 |
| Si x∈]1;2] | F(x)=p(X=0)+p(X=1)=0,3 |
| Si x∈]2;3] | F(x)=p(X=0) +p(X=1) +pX=2)=0,7 |
| Si x∈]3;4] | F(x)=p(X=0) + p(X=1) +p(X=2)+p(X=3)=0,9 |
| Si x∈]4;+∞[ | F(x)=1 |
2) la courbe représentative (CF)