تمرين 1 tp

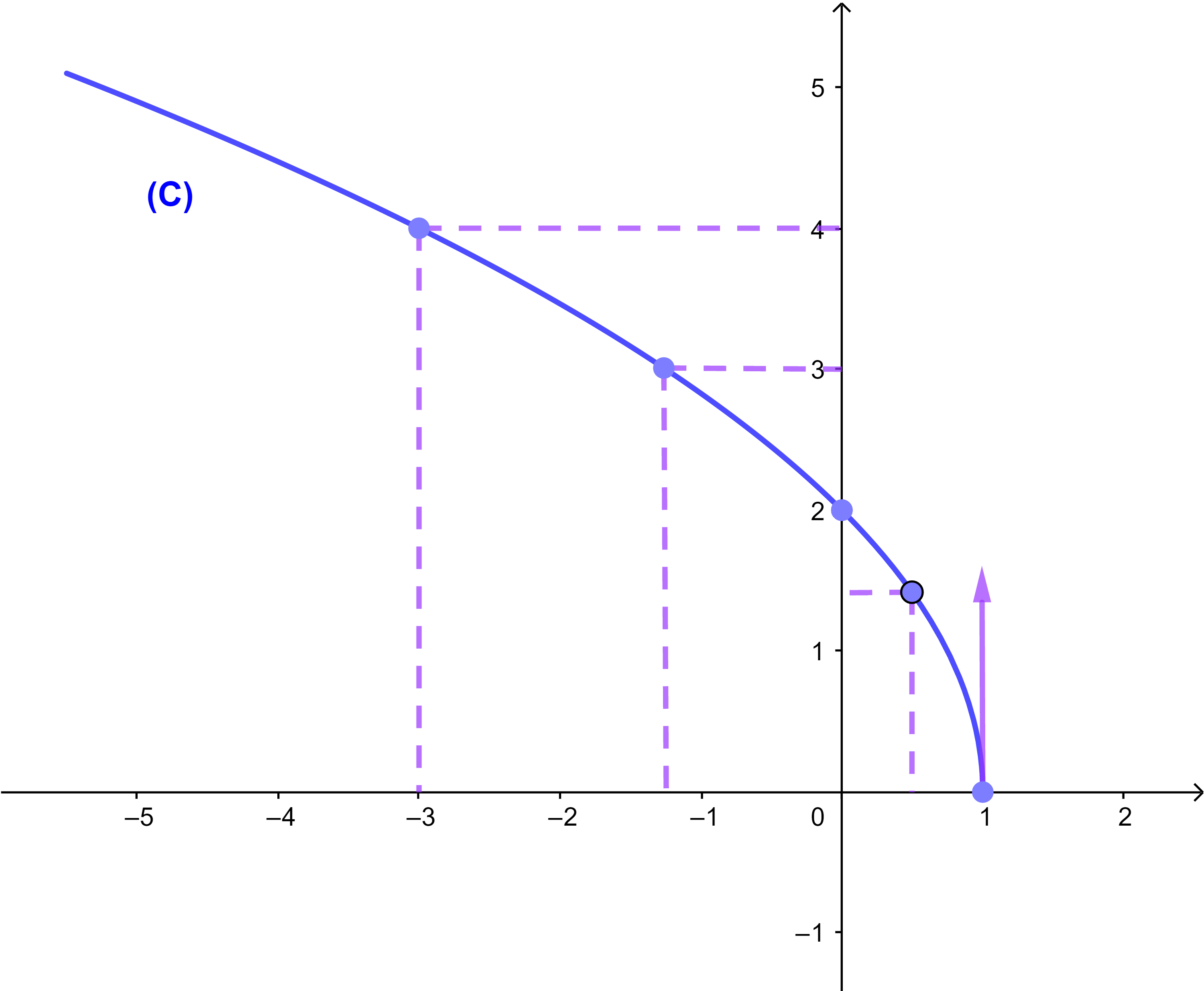
لتكن f دالة عددية معرفة كما يلي f(x)=√(4x+8)
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i^→;j^→).
1) حدد D مجموعة تعريف الدالة f
2) احسب النهاية

lim +∞

f(x)

3) احسب f'(x) حيث x∈D وادرس اشارتها
4) استنتج رتابة الدالة f وانشئ جدول تغيراتها
5) انشئ المنحنى (C).

تصحيح

1) f معرفة اذا كان 4x+8≥0 اي اذا كان x≥-2
ومنه فان D=[-2;+∞[
2) نهاية f(x) عند +∞

lim +∞

4x + 8 =

lim +∞

4x = +∞

lim +∞

f(x)

= +∞

اذن

3) f قابلة للاشتقاق اذا كان 4x+8>0
اي x>-2 أي x∈]-2;+∞[.

ليكن x∈]-2;+∞[

f '(x) =	(4x + 8)'
	2√(4x + 8)
=	4
	2√(4x + 8)

∀x∈]-2;+∞[: f '(x) =	2	اذن
	√(4x + 8)

2>0 و 2 √(4x+8)>0
اذن (∀x∈D) / f'(x)>0

4) بماأن (∀x∈D) / f'(x)>0
فان f تزايدية قطعا على ]-2;+∞[
جدول تغيرات للدالة f

x	-2		+∞
f '(x)	||	+
f	0	↗	+∞

5) منحنى الدالة f

تمرين 2 tp

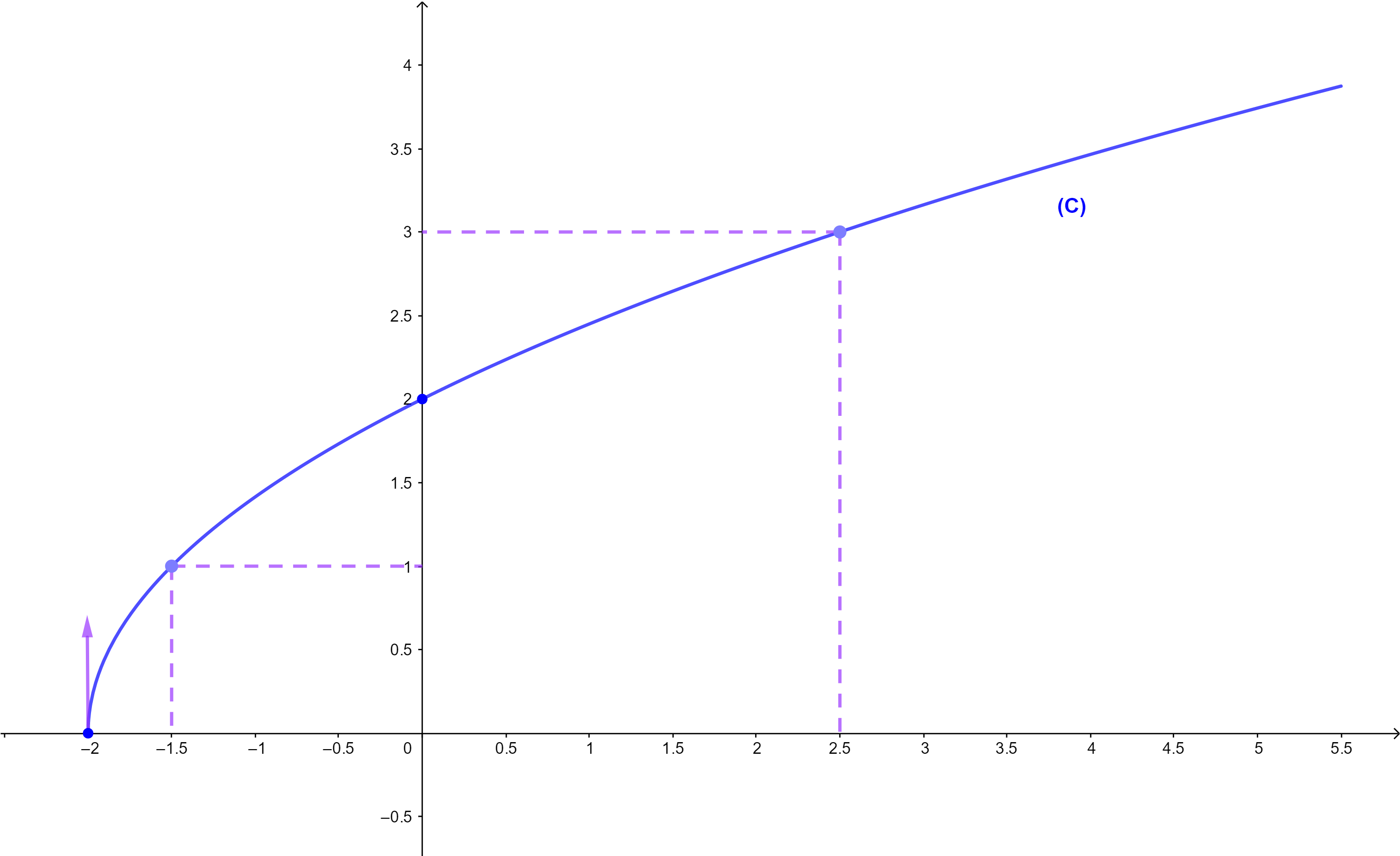
لتكن f دالة عددية معرفة كما يلي f(x)=√(-4x+4) و (C) المنحنى الممثل لها في معلم متعامد ممنظم (O;i^→;j^→).
1) حدد D مجموعة تعريف الدالة f
2) احسب النهاية

lim -∞

f(x)

3) احسب f'(x) حيث x∈D وادرس اشارتها
4) استنتج رتابة الدالة f وانشئ جدول تغيراتها
5) انشئ المنحنى (C)

تصحيح

1) f معرفة اذا كان -4x+4≥0
-4x≥-4 ⇔ 4x<4 ⇔ x<1
ومنه فان D=]-∞;1]
2) نهاية f(x) عند -∞

lim -∞

-4x + 4 =

lim -∞

- 4x = +∞

lim -∞

f(x)

= +∞

اذن

3) f قابلة للاشتقاق اذا كان -4x+4>0
اي x<1 أي x∈]-∞;1[.

f'(x) =	(-4x + 4)'
	2√(-4x + 4)
=	-4
	2√(-4x + 4)

(∀x∈]-∞;1[)/ f'(x) =	-2	اذن
	√(- 4x + 4)

-2<0 و √(-4x+4)>0
اذن (∀x∈]-∞;1[) f'(x)<0.

4) لدينا (∀x∈]-∞;1[) f'(x)<0 اذن f تناقصية قطعا على ]-∞;1[.

x	-∞		1
f '(x)		-	||
f	+∞	↘	0

5) منحنى الدالة f