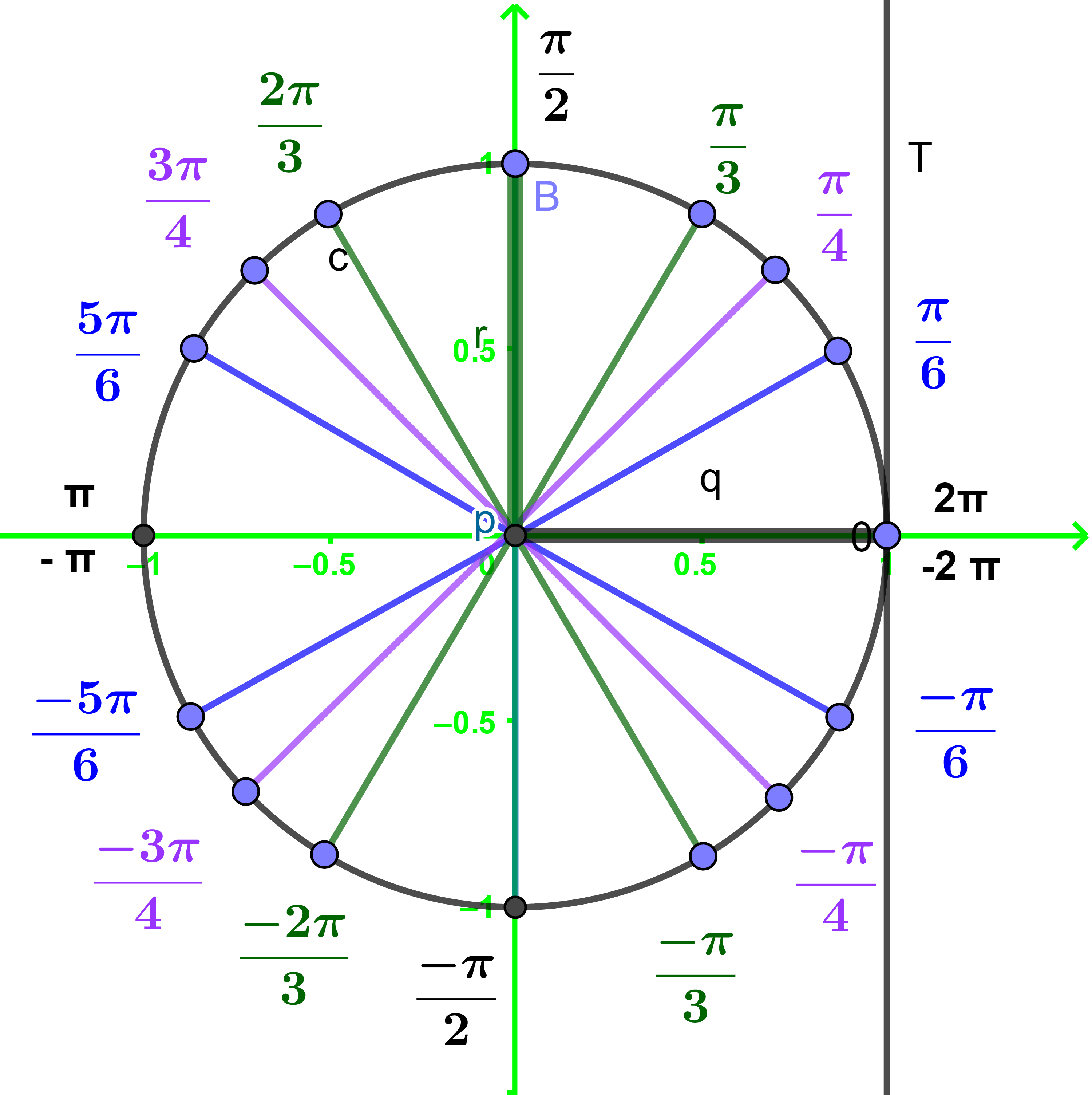
الحساب المثلثي (2_3)
تمرين 1 tp
حل في المجال I=[0;2π] المعادلتين
(E1):2cosx-√2=0
(E2): 2cosx-1=0.
تمرين 2 tp
حل في I=]-2π;2π] المعادلة
(E):2sinx = √2.
تصحيح
اولا نحل المعادلة (E) في IR.
| sinx = | √2 | تعني (E) |
| 2 |
| sin( | π | ) = | √2 | نعلم ان |
| 4 | 2 |
اذن (E) تكافئ
| sin x = sin | π |
| 4 |
تكافئ
| أو | x = | π | +2kπ | (k و k'∈ℤ) |
| 4 | ||||
| x = π- | π | +2k'π | ||
| 4 |
ثانيا نؤطر هذه الحلول في المجال I=[-2π;2π]
| -2π≤ | π | +2kπ | ≤2π | (a) |
| 4 | ||||
| -2≤ | 1 | +2k | ≤2 | يعني |
| 4 |
| -2 - | 1 | ≤+2k≤ 2- | 1 | يعني |
| 4 | 4 | |||
| -9 | ≤k≤ | 7 | يعني | |
| 8 | 8 |
k∈ℤ اذن k=-1 او k=0
| x = | π | +2kπ | (k∈ℤ) لدينا |
| 4 |
| x = | π | او x = | -7π | ومنه فان |
| 4 | 4 |
| -2π ≤ | 3π | +2k'π ≤2π | (b) |
| 4 | |||
| -2 ≤ | 3 | +2k'≤2 | يعني |
| 4 |
| -2- | 3 | ≤ +2k' ≤ 2- | 3 | يعني |
| 4 | 4 |
يعني
| -11 | ≤k'≤ | 5 |
| 8 | 8 |
k'∈ℤ اذن (k'=-1 او k'=0)
| x = | 3π | +2k'π | (k'∈ℤ) لدينا |
| 4 |
| x = | 3π | او x= | -5π | ومنه فان |
| 4 | 4 |
وبالتالي مجموعة حلول المعادلة (E)
| S = { | -7π | ; | -5π | ; | π | ; | 3π | } |
| 4 | 4 | 4 | 4 |