3.2 L'inéquation cosx≥a

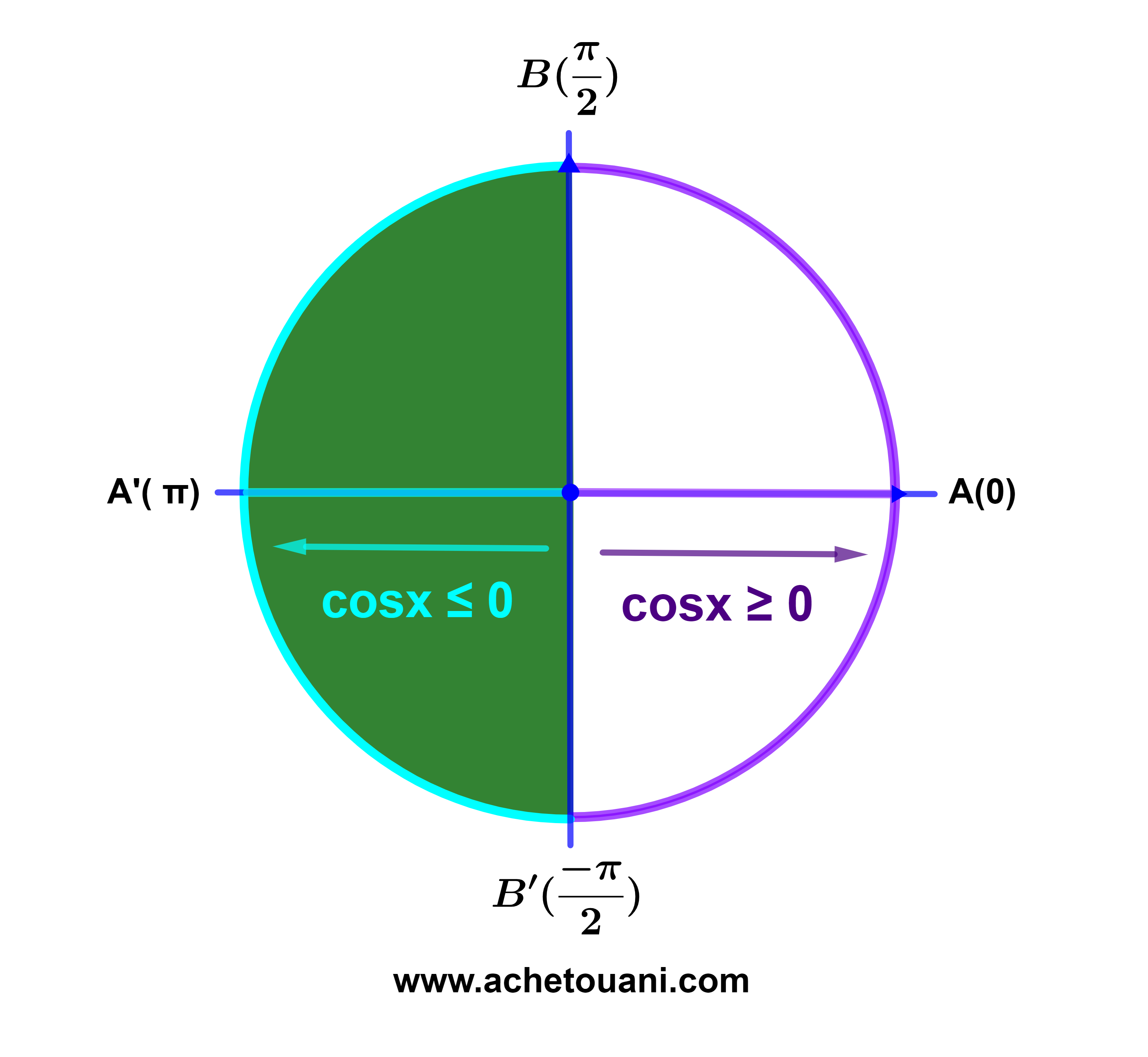
3.2.1 Propriété

Si x∈[	-π	;	π	]
	2		2

alors cosx≥0.

Si x∈[-π;	-π	] ∪ [	π	; π]
	2		2

alors cosx≤0.

En général

Si x∈[	-π	+2kπ;	π	+2kπ]
	2		2

alors cosx≥0.

Si x∈[-π+2kπ;	-π	+2kπ]
	2

alors cosx≤0.

Si x∈ [	π	+2kπ; π+2kπ]
	2

alors cosx≤0.

3.2.2 Exemple

Résoudre dans [0;π] l'inéquation
2cosx≥1.

Correction
1) On résout l'équation
(E) 2cosx=1 dans IR.

(E) signifie cosx =	1
	2

on a cos(	π	)=	1
	3		2

ou	x =	π	+2kπ	k et k'∈ℤ
		3
	x = -	π	+2k'π
		3

2) On encadre ces solutions dans I

(a) 0 ≤	π	+ 2kπ	≤ π
	3

0 ≤	1	+2 k	≤ 1
	3

Signifie

0 -	1	≤ + 2k≤ 1 -	1
	3		3

signifie

-1	≤ k ≤	2
6		6

k∈ℤ donc k=0 ainsi

x =	π
	3

(b) 0 ≤	-π	+ 2k'π	≤ π
	3

signifie

0 ≤	-1	+ 2k'	≤ 1
	3

signifie

0 +	1	≤ 2k'≤ 1 +	1
	3		3

Signifie

1	≤ k' ≤	4
6		6

k'∈ℤ, donc k' n'existe pas
3) On représente cette solution sur un axe ou sur le cercle trigonométrique (C).
(0)----(π/3)----(π/2)----(π)

S = [0 ;	π	]
	3