تمرين 1 tp

1) اتمم جدول تغيرات الدالة f حيث f دالة زوجية

x	-3		-1		0		1		3
f				↘	3		5	↘	-4

تصحيح

1) من خلال جدول تغيرات الدالة f يتبين أن
f(1)=5 اذن f(-1)=f(1)=5 لأن f زوجية
ولدينا f(3)=-4 فان f(-3)=f(3)=-4
اذن f(-3)=-4 و f(-1)=5.

2) من خلال جدول تغيرات f يتبين أن f تناقصية قطعا على المجال [1;3]
وبما أن f زوجية فانها تزايدية قطعا على المجال المماثل أي على المجال [-3;-1].
3) من خلال جدول تغيرات f يتبين أن f دالة تناقصية قطعا على المجال [-1;0]
وبما أنها دالة زوجية فانها تزايدية قطعا على المجال المماثل أي على المجال [0;1].
وبذلك نتمم جدول تغيرات الدالة f

x	-3		-1		0		1		3
f	-4	↗	5	↘	3	↗	5	↘	-4

تمرين 2 tp

1) اتمم جدول تغيرات الدالة f حيث f دالة فردية

x	-3		-1		0		1		3
f				↘	3		5	↘	-4

تصحيح

1) من خلال جدول تغيرات الدالة f يتبين أن
f(1)=5 وبما أن الدالة f فردية
فان f(-1)=-f(1)=-5.

ولدينا أيضا f(3)=-4 اذن f(-3)=-f(3)=-(-4)=4
ومنه فان f(-3)=4 و f(-1)=-5.
2) من خلال جدول تغيرات f يتبين أن f تناقصية قطعا على المجال [1;3]
وبما أنها f فردية فانها تناقصية قطعا على المجال المماثل أي على المجال [-3;-1]
3) من خلال جدول تغيرات f يتبين أن f دالة تناقصية قطعا على المجال [-1;0]
وبما أنها دالة فردية فانها تناقصية قطعا على المجال المماثل أي على المجال [0;1]
وبذلك نتمم جدول تغيرات الدالة f

x	-3		3
f	4	↘	-4

تمرين 3 tp

لتكن f دالة عددية معرفة كما يلي f(x)=2x و (C) منحناها في المعلم متعامد ممنظم (O;i^→;j^→).
انشئ المنحنى (C) واستنتج رتابتها مبيانيا.

تصحيح

لرسم المنحنى (C) يكفي تعيين قيم افاصيل مناسبة لبعض نقط المنحنى بواسطة الدالة لمعرفة شكل المنحنى (C)

x	- 1	0	1	2
f(x )	- 2	0	2	4

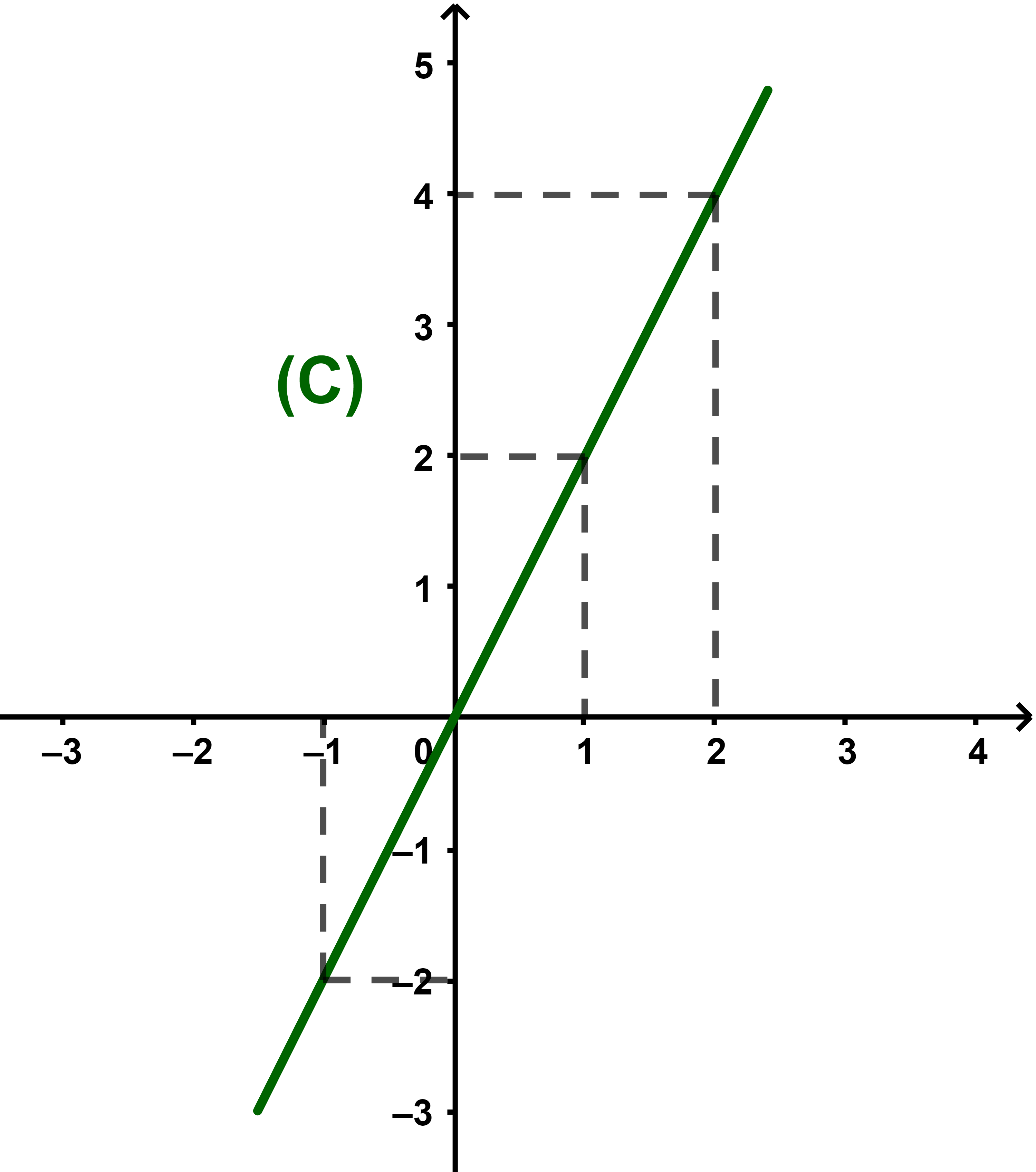
ملاحظة نقط المنحنى (C) مستقيمية لان معادلة المنحنى
y = 2x هي معادلة مستقيم مار من أصل المعلم

نحدد تغيرات الدالة f من خلال المنحنى
الدالة f تزايدية قطعا على IR

x	-∞		+∞
f		↗