تمرين 1 tp

لتكن f دالة عددية معرفة على IR بما يلي

{	f(x) = 2x	x ≥ 1
	f(x) = x + 1	x < 1

و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i^→;j^→) انشئ المنحنى (C).

تصحيح

f دالة عددية معرفة بالاجزاء
اذا كان x∈]-∞;1[ فان f(x)=x+1.
اذا كان x∈[1;+∞[ فان f(x)=2x.

المنحنى (C) هو اذن اتحاد نصفي مستقيم.

(D1): y=x+1 / x< 1

(D2): y=2x / x≥1

تمرين 2 tp

لتكن f دالة عددية معرفة على IR بما يلي

{	f(x) = 2x + 1	x ≥ -2
	f(x) = -7 - 3x	x < -2

و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i^→;j^→). انشئ النحنى (C).

تصحيح

f دالة عددية معرفة بالاجزاء
1) اذا كان x∈ ]-∞;-2[ فان f(x)=-7-3x
اذا كان x∈ [-2;+∞[ فان f(x)=2x+1
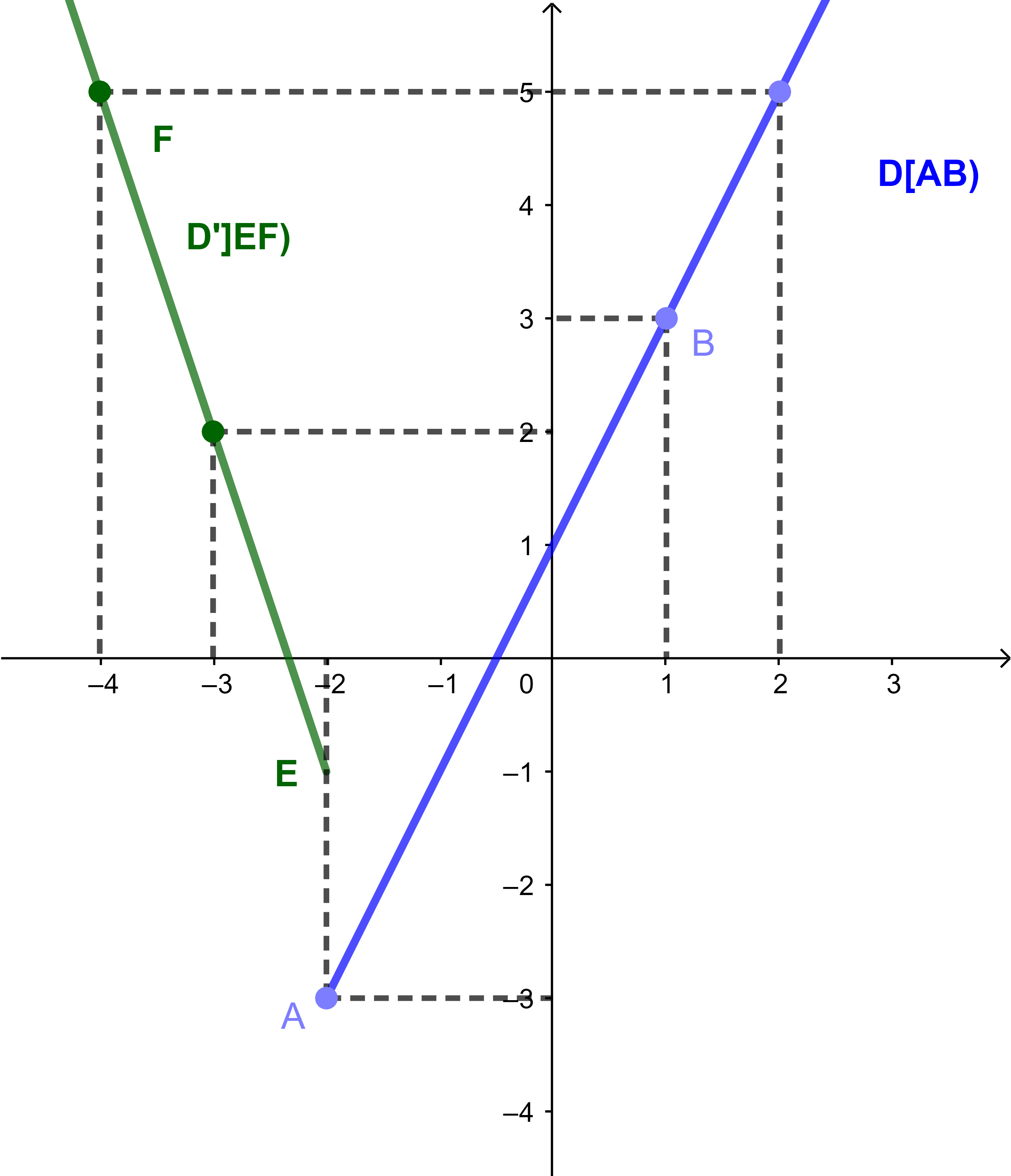
وبالتالي منحنى الدالة f اذن هو اتحاد نصفي مستقيم
(D): y=-7-3x / x < -2
(D'): y=2x+1 / x≥-2.

تمرين 3 tp

f دالة عددية معرفة على IR بما يلي f(x)=-2x²
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i^→;j^→).
انشئ النحنى (C) استنتج مبيانيا رتابة الدالة f.

تصحيح

1) f دالة حدودية اذن D=IR
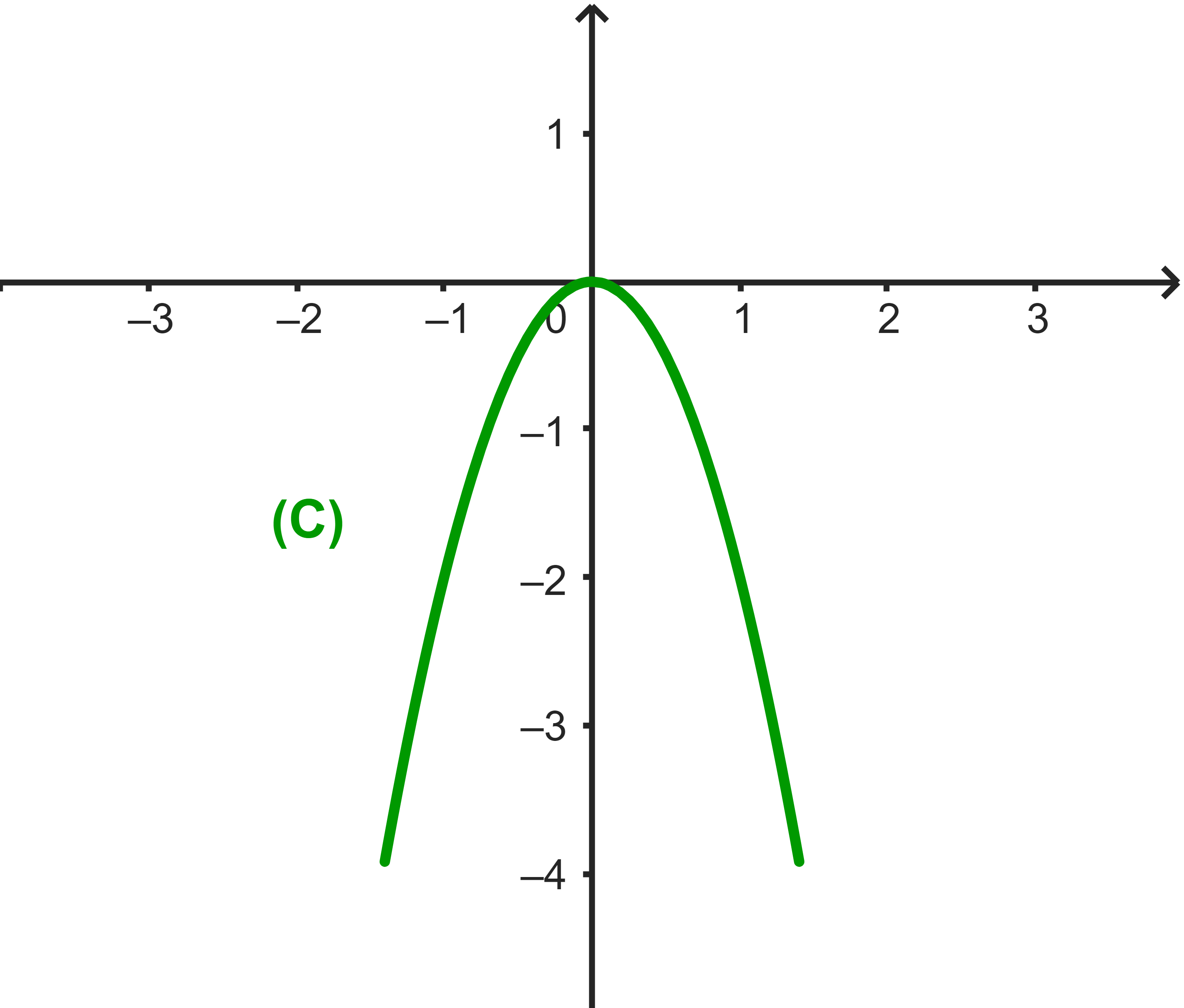
لرسم المنحنى (C) يكفي تعيين قيم افاصيل مناسبة لبعض نقط المنحنى بواسطة الدالة لمعرفة شكل المنحنى (C)

x		-1	-1/2	0	1/2	1
f(x)		-2	-1/2	0	-1/2	-2

2) الدالة f تناقصية قطعا على المجال IR⁺=[0;+∞[
وتزايدية قطعا على المجال IR^-=]-∞;0]

جدول التغيرات

x		-∞		0		+∞
f			↗	0	↘

و f(0)=0 هي القيمة القصوى للدالة f.