الدوال العددية (4)
2- التمثيل المبياني للدالة x→ax²+bx+c
2.1 الدالة x→ax²
2.1.1 أمثلة
مثال 1
لتكن f دالة عددية معرفة على IR بما يلي f(x)=x²
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i→;j→).
انشئ النحنى (C).
تصحيح
f دالة حدودية اذن D=IR.
نحدد بعض صور مناسبة بواسطة الدالة لمعرفة شكل منحنى الدالة f
| x | -2 | -1 | 0 | 1/2 | 1 | 2 | 3 |
| f(x) | 4 | 1 | 0 | 1/4 | 1 | 4 | 9 |
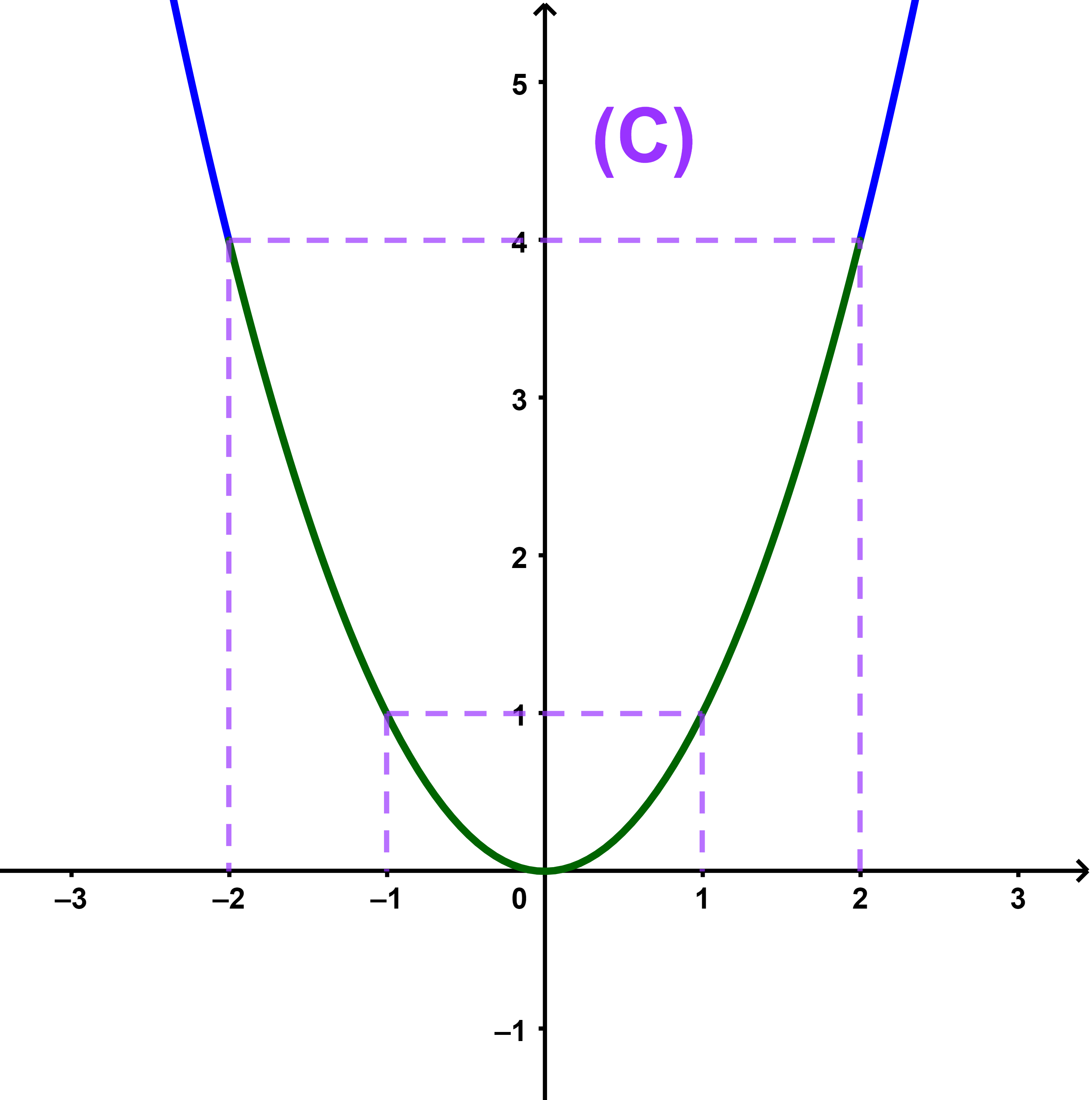
هذا المنحنى يسمى شلجما محوره هو محور الاراتيب (Oy) موجه الى الاعلى.
انطلاقا من المنحنى
الدالة f تزايدية قطعا على المجال IR+=[0;+∞[
وتناقصية قطعا على المجال IR-=]-∞;0]
و f(0)=0 هي القيمة الدنيا للدالة f.
جدول التغيرات
| x | -∞ | 0 | +∞ | |||
| f | ↘ | 0 | ↗ |
مثال 2
f دالة عددية معرفة على IR بما يلي
f(x)=-2x²
و (C) المنحنى الممثل لها في معلم متعامد ممنظم
(O;i→;j→).
انشئ النحنى (C).
تصحيح
f دالة حدودية اذن D=IR.
نحدد بعض صور مناسبة بواسطة الدالة لمعرفة شكل منحنى الدالة f
| x | -1 | -1/2 | 0 | 1/2 | 1 |
| f(x) | -2 | -1/2 | 0 | -1/2 | -2 |
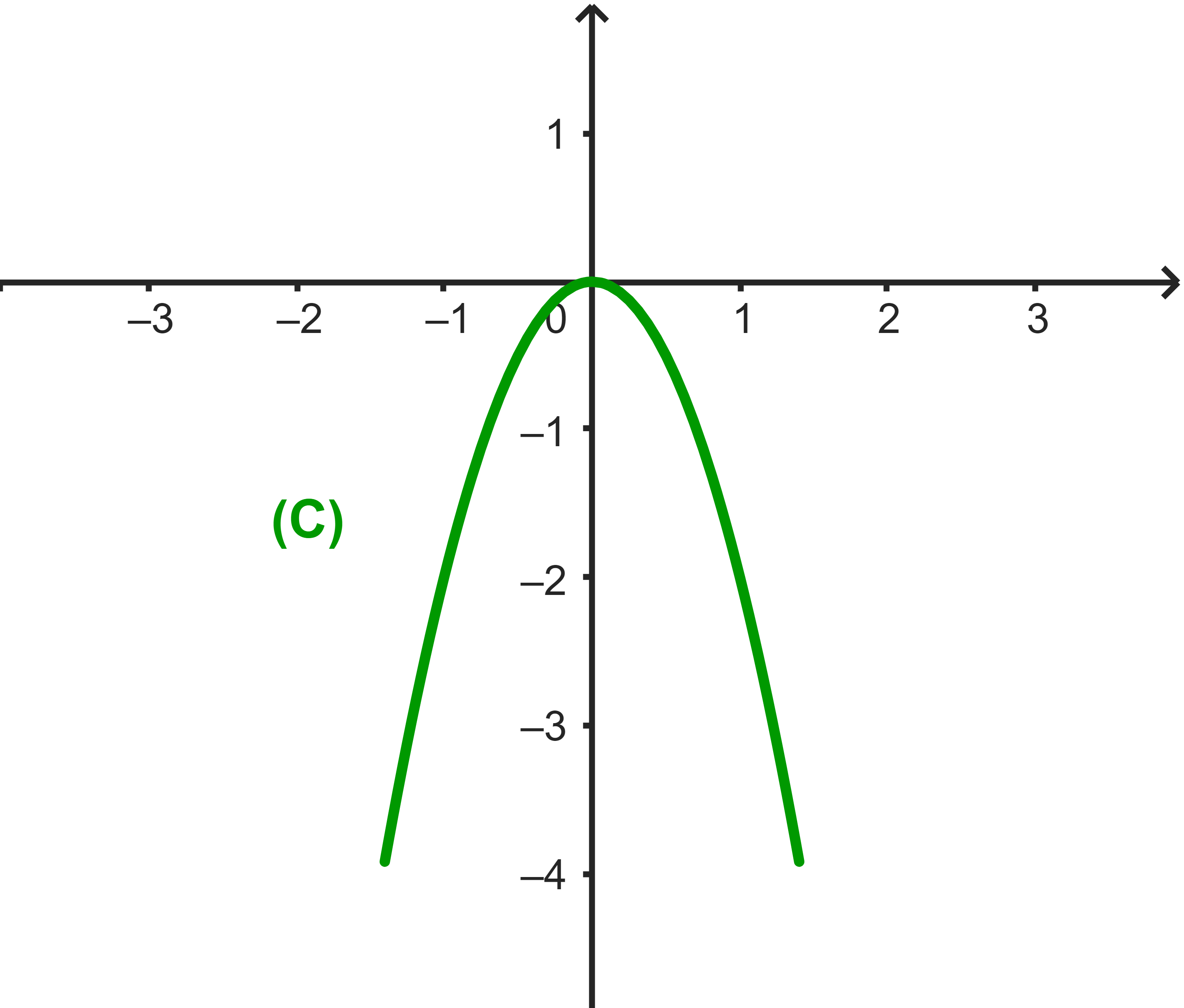
انطلاقا من المنحنى الدالة f تناقصية قطعا على المجال
IR+=[0;+∞[
وتزايدية قطعا على المجال
IR-=]-∞;0].
و f(0)=0 هي القيمة القصوى للدالة f.
جدول التغيرات
| x | -∞ | 0 | +∞ | |||
| f | ↗ |
0 | ↘ |