Exercice 1 tp

Le plan est rapporté au repère orthonormé (O;i^→;j^→)
Déterminer graphiquement les coordonnées des points A, B; C; D ; E.

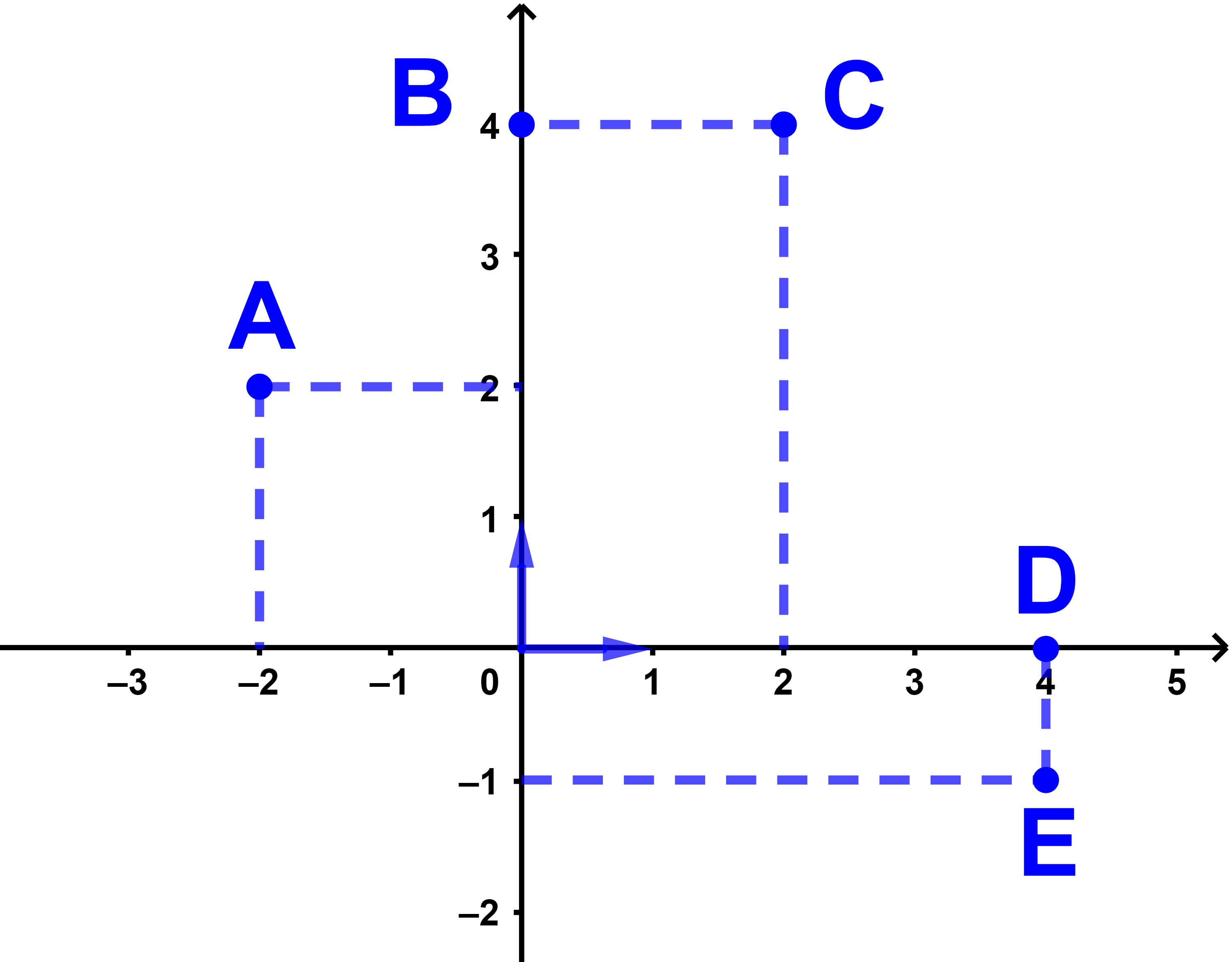
Exercice 2 tp

Le plan est rapporté au repère orthonormé (O;i^→;j^→)
u^→(3;2) و v^→(-2;5) sont deux vecteurs
Déterminer les coordonnées des vecteurs
u^→+v^→ et 4u^→-v^→

Correction

On a u^→+v^→(3+(-2);2+5) donc u^→+v^→(1;7)
et on a 4u^→(4.3;4.2) donc 4u^→(12;8)
ainsi 4u^→-v^→(12-(-2);8-5)
alors 4u^→-v^→(14;3).

Exercice 3 tp

Dans le plan rapporté au repère orthonormé (O;i^→;j^→) on considère trois points
E(2;3); F(4;8) ; G(-2;5)
Déterminer EF^→ ; EG^→ ; GF^→.

Correction

On a EF^→(4-2;8-3), donc EF^→(2;5)
on a EG^→(-2-2;5-3) donc EG^→(-4;2)
et on a GF^→(4-(-2);8-5) donc EF^→(8;3).

Exercice 4 tp

Dans le plan est rapporté au repère orthonormé (O;i^→;j^→) on considère les points
E(3;7) ; F(-1;1) ; G(3;5) ; H(-7;-3)
1) Vérifier que I(1 ; 4) est milieu du segment [EF]
2) Vérifier que J(-2 ; 1) est milieu du segment [GH]
3) Déterminer la distance IJ

Correction

1) On vérifie que I est milieu de [EF]

xi =	3 + (-1)		yi =	7 + 1
	2			2
=	2		=	8
	2			2

donc x_i = 1 et y_i = 4
ainsi I(1 ; 4) est milieu du segment [EF]

2) On vérifie que J est milieu de [EF]

xj =	3 + (-7)		yj =	5 + (-3)
	2			2
=	-4		=	2
	2			2

Donc x_j = -2 et y_j = 1
ainsi J(-2 ; 1) est milieu du segment [EF]
3) On calcule la distance IJ
on a IJ^→(-2 -(1) ; 1 - 4) donc IJ( -3 ; -3)
ainsi IJ = √((-3)² + (-3)²) = √(2 . 9)
alors IJ = 3√(2)

Exercice 5 tp

Dans le plan rapporté au repère orthonormé (O;i^→;j^→) on considère les points
A(2;1) ; B(-1;1) ; C(2;4)
1) Montrer que le triangle ABC est isocèle
2) Déterminer I le milieu du segment [BC]

Correction

1) On calcule la distance AB
On a AB^→(-1 - 2 ; 1 - 1) donc AB^→(-3 ; 0)
ainsi AB = √((-3)² + 0²) = √(9) = 3

On calcule la distance AC
On a AC^→(2 - 2;4 - 1) donc AC^→(0;3)
ainsi AC=√(0²+(3)²)=√(9)=3
Puisque AB = AC alors ABC est un triangle isocèle de sommet A
2) On détermine I le milieu du segment [BC]

xi =	-1 + 2	; yi =	1 + 4
	2		2

donc I(	1	;	5	)
	2		2

est milieu du segment [BC]