تمرين 1 tp

المستوى منسوب الى معلم متعامد ممنظم (O;i^→;j^→)
حدد احداثيتات النقط A, B; C; D ; E انطلاقا من المعلم

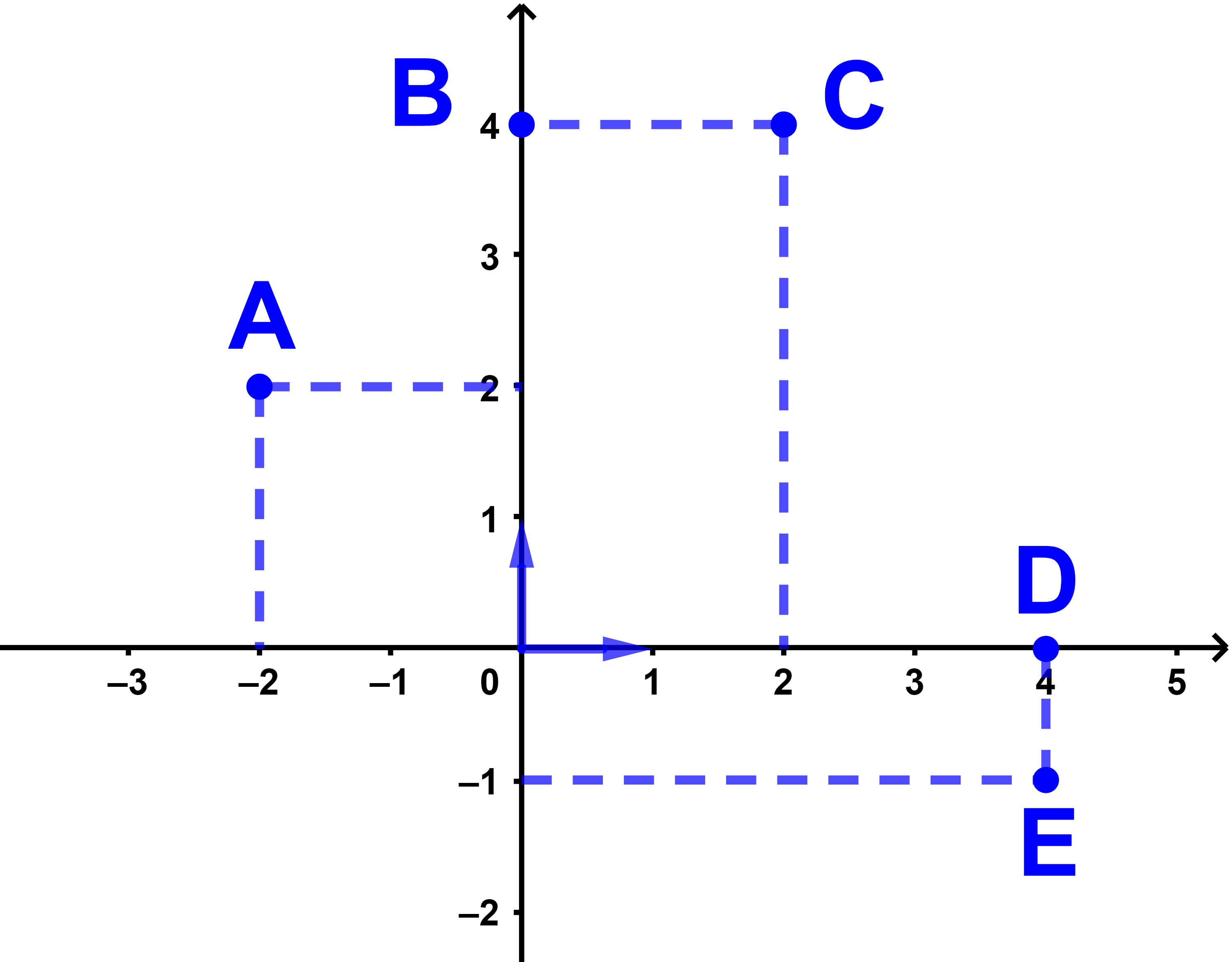
تمرين 2 tp

المستوى منسوب الى معلم متعامد ممنظم
(O;i^→;j^→). لتكن u^→(3;2) و v^→(-2;5) متجهتين.
حدد احداثيتات u^→+v^→ و 4u^→-v^→.

تصحيح

لدينا u^→ + v^→(3+(-2) ; 2+5)
اذن u^→ + v^→(1 ; 7)
ولدينا 4u^→(4.3 ; 4.2) اذن 4u^→(12 ; 8)
ومنه فان 4u^→ - v^→(12-(-2) ; 8-5)
وبالتالي 4u^→-v^→(14 ; 3)

تمرين 3 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→)
نعتبر ثلاث نقط E(2 ; 3); F(4 ; 8) ; G(-2 ; 5)
حدد EF^→ ; EG^→ ; GF^→

تصحيح

لدينا EF^→(4-2 ; 8-3), ومنه فان EF^→(2 ; 5)
لدينا EG^→(-2-2 ; 5-3) اذن EG^→(-4 ; 2)
ولدينا GF^→(4-(-2);8-5) اذن EF^→(8;3)

تمرين 4 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) نعتبر النقط
E(3 ; 7) ; F(-1 ; 1) ; G(3 ; 5) ; H(-7 ; -3)
1) تحقق ان النقطة I(1 ; 4) منتصف القطعة [EF]
2) تحقق ان النقطة J(-2 ; 1) منتصف القطعة [GH]
3) حدد المسافة IJ

تصحيح

1) نتحقق ان I منتصف [EF]

xi =	3 + (-1)		yi =	7 + 1
	2			2
=	2		=	8
	2			2

اذن x_i = 1 و y_i = 4 ومنه فان
I(1 ; 4) منتصف القطعة [EF]

2) نتحقق ان J منتصف القطعة [EF]

xj =	3 + (-7)		yj =	5 + (-3)
	2			2
=	-4		=	2
	2			2

اذن x_j = -2 و y_j = 1 ومنه فان
J(-2 ; 1) منتصف القطعة [EF]
3) نحسب المسافة IJ
لدينا IJ^→(-2 -(1) ; 1 - 4) اذن IJ( -3 ; -3)
ومنه فان IJ = √((-3)² + (-3)²) = √(2 . 9)
وبالتالي IJ = 3√(2)

تمرين 5 tp

في المستوى المنسوب الى معلم متعامد ممنظم
(O ; i^→ ; j^→) نعتبر النقط
A(2 ; 1) ; B(-1 ; 1) ; C(2 ; 4)
1) بين أن المثلث ABC متساوي الساقين
2) حدد I منتصف القطعة [BC]

تصحيح

1) نحسب المسافة AB
لدينا AB^→(-1 - 2 ; 1 - 1) اذن AB^→(-3 ; 0)
ومنه فان AB = √((-3)² + 0²) = √(9) = 3

نحسب المسافة AC
لدينا AC^→(2 - 2 ; 4 - 1) اذن AC^→(0 ; 3)
ومنه فان AC = √(0² + (3)²) = √(9) = 3
وبما أن AB = AC فان المثلث ABC متساوي الساقين رأسه A
2) نحدد I منتصف القطعة [BC]

xi =	-1 + 2	; yi =	1 + 4
	2		2

I(	1	;	5	) اذن
	2		2

منتصف القطعة [BC]