المستقيم في المستوى (7)
2.2 توازي وتعامد مستقيمات
2.2.1 تعريف
المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i→;j→).
ليكن (D) مستقيم معرف بنقطة وميله m.
المعادلة المختصرة للمستقيم (D) هي معادلة تكتب على الشكل
y=mx+p حيث p هو الارتوب عند الاصل.
2.2.2 التوازي
المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i→;j→).
ليكن (D) و (D') مستقيمين من المستوى.
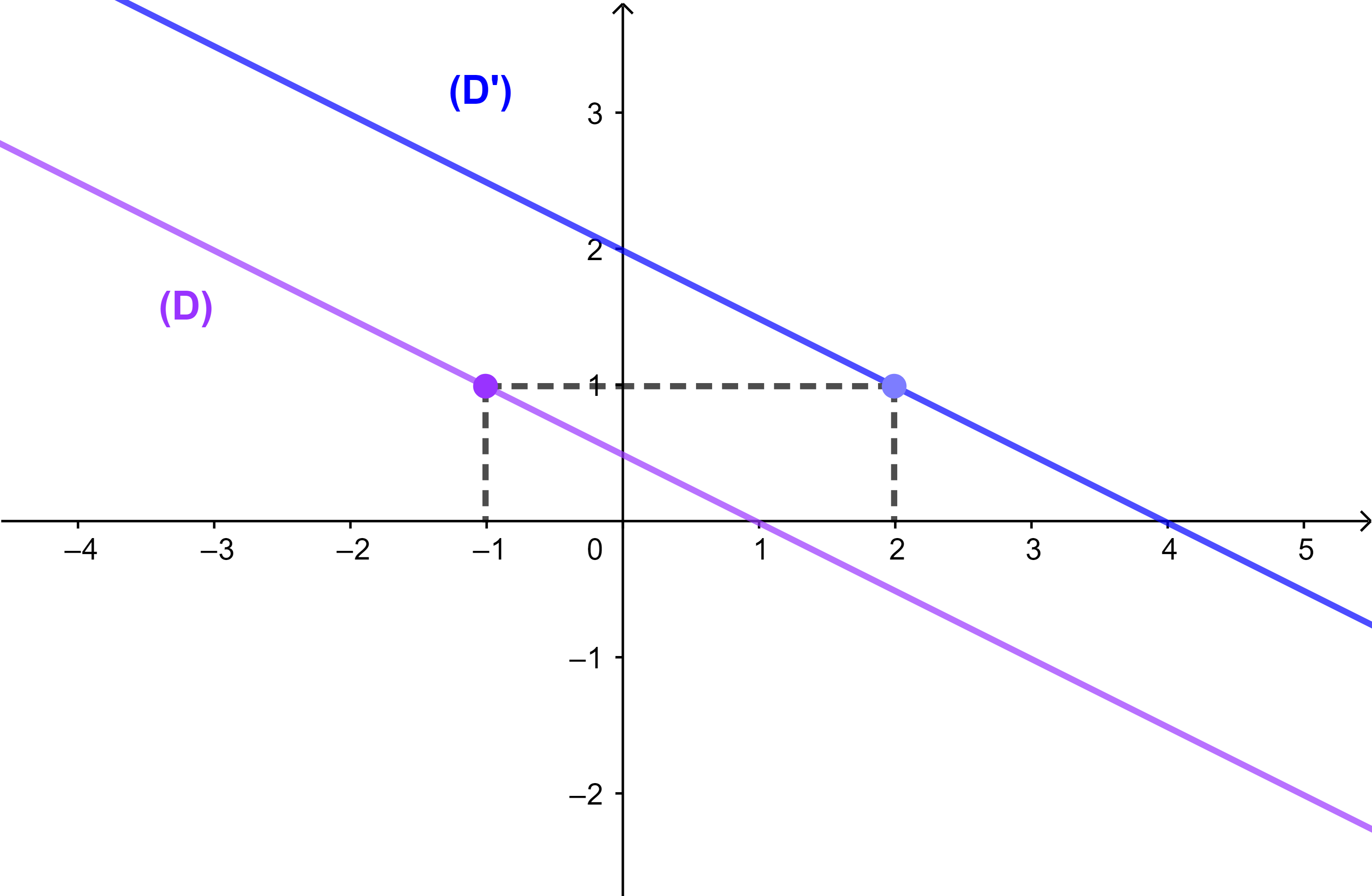
يكون (D) و (D') متوازيين ونكتب (D)||(D') اذا كان لهما نفس الميل.
مثال
ليكن (D): y=2x+1 و (D"): 2x-y-3=0 مستقيمين في المستوى.
بين ان (D)||(D").
تصحيح
لدينا (D"): 2x-y+3=0 يكافـئ y=2x-3
اذن m"=2 ميل المستقيم (D")
وبما ان m=m" فان (D)||(D").
2.2.3 التعامد
المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i→;j→).
(D) و (D') مستقيمان متعامدان ونكتب (D)⊥(D')
اذا كان جذاء ميلهما يساوي
-1.
مثال 1
ليكن (D): x-y+2=0 و (D'): x+y-4=0 مستقيمين
نبين ان (D)⊥(D').
لدينا x-y+2=0 يكافـئ y=x+2 اذن ميل (D) هو m=1
وايضا x+y-4=0 يكافـئ y=-x+4 اذن ميل (D') هو m'=-1
وبما ان m.m'=-1 فان (D)⊥(D').

تمرين 1 tp
المستوى ℙ منسوب الى معلم متعامد ممنظم
(O;i→;j→).
(D): x-4y+4=0 و (D'): 4x+y+1=0 مستقيمان في المستوى.
بين ان (D)⊥(D').
تصحيح
لدينا x-4y+4=0 يكافـئ 4y=x+4
يكافـئ
| y = | 1 | x + 1 |
| 4 |
| m = | 1 | اذن |
| 2 |
ميل المستقيم (D).
ولدينا
4x+y+1=0 يكافـئ y=-4x-1
اذن (D') ميله m'=-4
وبما ان m.m'=-1 فان (D)⊥(D').