Rappel
Théorème de Rolle Soit f une fonction définie sur un intervalle I=[a;b].
Si f vérifie les trois conditions suivantes.
(1) f est continue sur le segment [a;b].
(2) f est dérivable sur l'intervalle ouvert ]a;b[.
(3) f(a) = f(b)
alors il existe c∈]a;b[ tel que f'(c)=0.

Théorème des accroissements finis (TAF) Soit f une fonction définie sur un intervalle I=[a;b].
Si f vérifie les deux conditions suivantes
(1) la fonction f est continue sur le segment [a;b].
(2) la fonction f est dérivable sur l'intervalle ouvert ]a;b[
alors il existe c∈]a;b[ tel que
f(b)-f(a)=f'(c)(b-a).

Inégalité des accroissements finis Soit f une fonction définue
sur un intervalle I=[a;b].
Si f vérifie les trois conditions suivantes
(1) f est continue sur le segment [a;b].
(2) f est dérivable sur l'intervalle ouvert ]a;b[.
(3) ∃(m;M)∈IR² tel que
∀x∈]a;b[: m≤f'(x)≤M
alors m(b-a)≤f(b)-f(a)≤M(b-a).

Exercice 1 tp

Soit f une fonction définue sur un intervalle
I=[1;4] par
f(x)=2+(x-1)(x-2)(x-3)(x-4).
Est ce que la fonction f vérifie les condtions du théorème de Rolle sur I ?

Correction

1) f est une restriction d'un polynôme donc continue sur l'intervalle I.
2) f est une restriction d'un polynôme donc dérivable sur I en particulier sur ]1;4[.
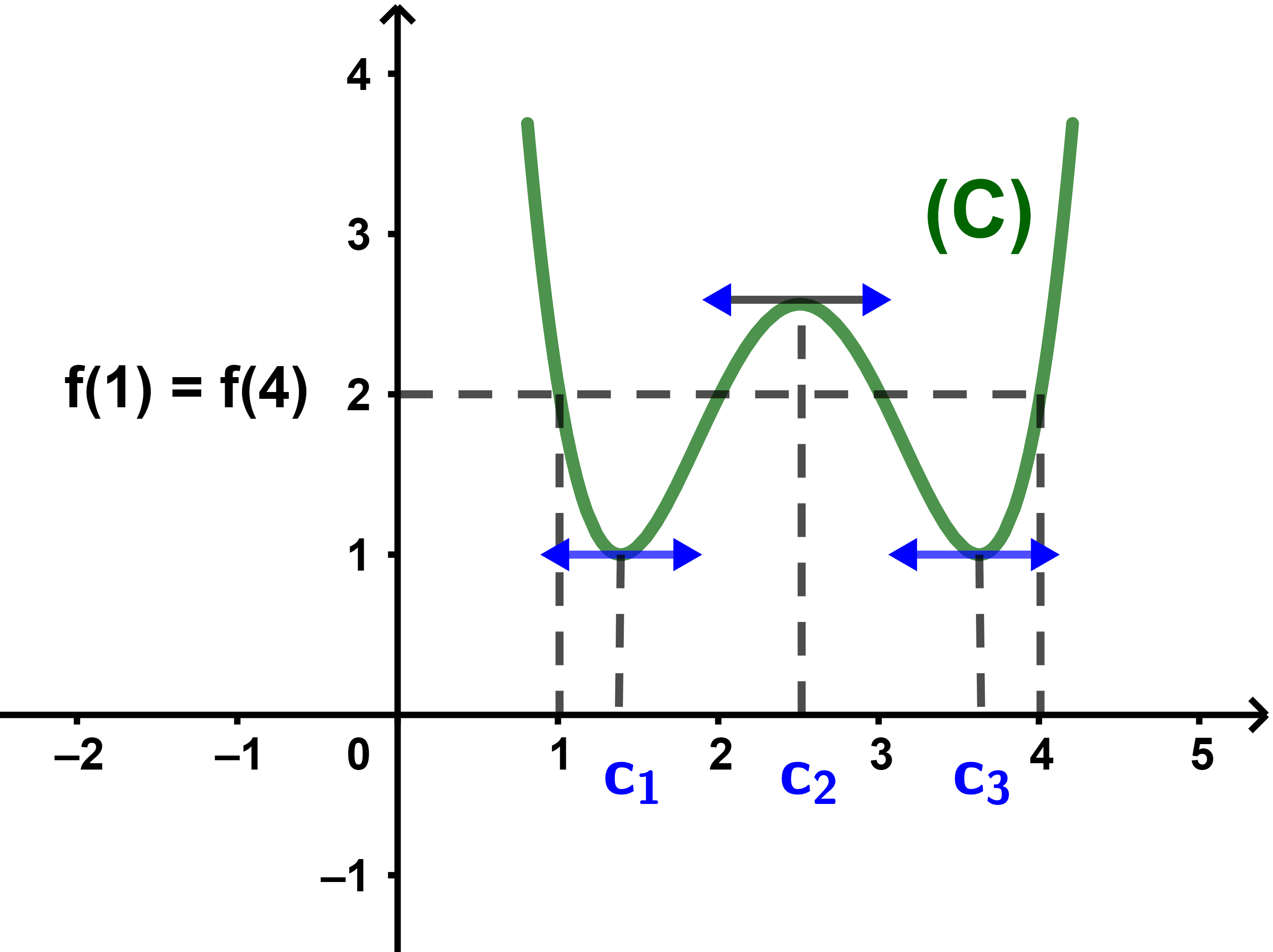
3) f(1)=2 et f(4)=2
donc f(1)=f(4) et donc la fonction f vérifie les conditions du théorème de Rolle
ainsi ∃c∈]1;4[ tel que f'(c)=0.

Exercice 2 tp

Est ce que la fonction f définie
sur l'intervalle I=[-√(3);√(3)] par
f(x)=x³-3x vérifie les condtions du théorème de Rolle ?

Correction

(1) f est une restriction d'un polynôme donc continue sur l'intervalle I.
(2) f est une restriction d'un polynôme donc dérivable sur I
en particulier sur ]-√(3);√(3)[.
(3) f(-√(3))=-3√(3)-(3(-√(3))=0.

f(√(3))=3√(3)-3√(3)=0
donc f(-√(3))=f(√(3))
et donc f vérifie les conditions du théorème de Rolle
ainsi (∃c∈]-√(3);√(3)[): f'(c)=0.
Vérification On a f'(x)=3x²-3
f'(x)=0 ⇔ 3(x-1)(x+1)=0
⇔ x=-1 ou x=1
-1 ; 1∈]-√(3);√(3)[ ; f'(-1)=0 et f'(1)=0
donc c existe dans l'intervalle ouvert
]-√(3);√(3)[.