8- الفانون الحداني

8.1 تذكير

اذا كانت تجربة مكونة من تكرار نفس الاختبار n مرة و E حدث من هذا الاختبار فان احتمال تحقيق الحدث E بالضبط k مرة حيث k≤n معرف كما يلي :
C^k_n (p(E))^k.(1-p(E))^n-k

8.2 خاصية

اذا كان المعغير العشوائي x معرفا بعدد مرات تحقيق الحدث E فان
p(x=k)=C^k_n (p(E))^k.(1-p(E))^n-k حيث k≤n
هذا المتغير العشوائي يسمى توزيعا حدانيا او متغير عشوائي وسيطاه n و p(E)

تمرين

يحتوي صندوق على 3 اقراص حمراء وقرصان خضروان , نسحب عشوائيا قرصا من الصندوق
1. احسب احتمال سحب قرصا اخضرا v
2. نكرر هذا الاختبار 3 مرات ونعتبر المتغير العشوائي x المعرف بعد مرات تحقق الحدث v
حدد قانون احتمال x

تصحيح :

p(v)= 2/5
x(w)={0;1;2;3}
p(x=0) = C°₃(2/5)°.(3/5)³ = 27/125 ; p(x=1)= C¹₃(2/5).(3/5)² = 54/125
p(x=2)= C²₃ (2/5)²(3/5) = 36/125 ; p(x=3)=C³₃ (2/5)³(3/5)° = 8/125

xi	0	1	2	3	المجموع
p(x=xi)	27/125	54/125	36/125	8/125	1

8.3 خاصية

الامل الرياضي والمغايرة والنحراف الطرازي معرفة كما يلي
E(x)=n.p(E) ; V(x)= n.p(E).(1-p(E)) و σ(x)=√(V(x))

مثال

8.4 دالة التجزيئ

8.4.1 تعريف

ليكن (w;p) فضاء احتماليا منتهيا و x متغيرا عشوائيا معرفا على w و x(w)={x1;x2;...;xq}
دالة التجزيئ للدالة F معرفة من IR الى [0;1] بما يلي F(x)=p(X< x)
∀x∈]xi;xi+1]; F(x)=p(X=x1)+p(X=x2) +...+ p(X=xi)
لماذا p(X=xi) وليس p(X=xi+1) لان X< x ; xi+1∈]xi;xi+1]

x	F(x)=p(X< x)
]-∞;x1]	0
]x1;;x2]	p(X=x1)
]x2;;x3]	p(X=x1)+p(X=x2)
..	..
]xn-1;;xn]	p(X=x1)+p(X=x2) +..+ p(X=xn-1)
]xn;;+∞[	1

8.4.2 مثال

نعود مرة اخرى الى المثال

x	F(x)=p(X< x)
]-∞;0]	0
]0;;1]	p(X=0)=8/27
]1;;2]	p(X=0)+p(X=1)=20/27
]2;3]	p(X=0)+p(X=1)+p(X=2)=26/27
]3;;+∞[	1

تمرين

الجدول التالي يحدد قانونا احتماليا منتهيا متغيره العشوائي X

xi	0	1	2	3	4
p(X=xi)	0,2	0,1	0,4	0,2	0,1

1) حدد F دالة التجزيئ للمتغير العشوائي X.
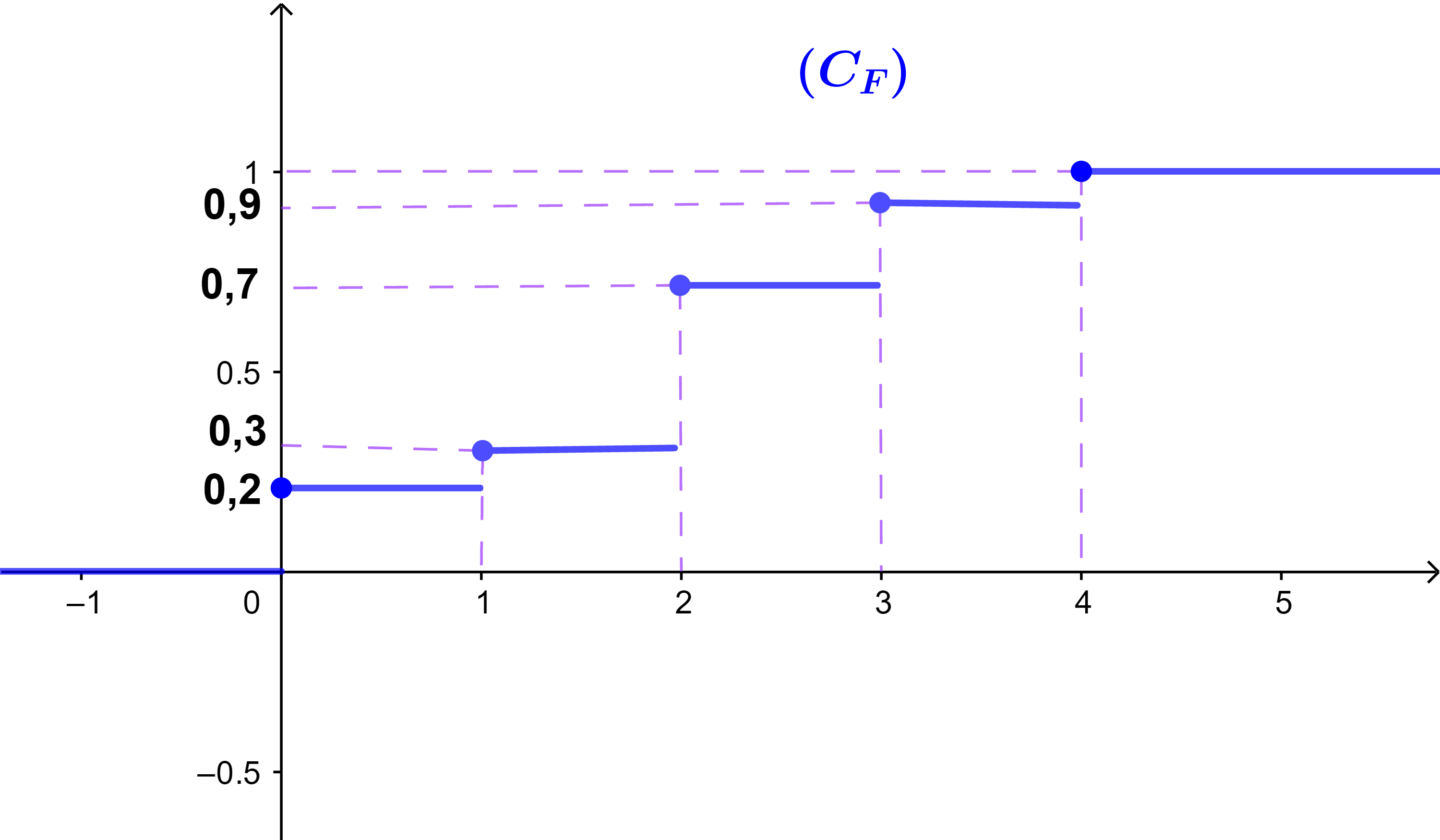
2) انشئ في معلم متعامد منحنى دالة التجزيئ F

تصحيح

1) نذكر ان F معرفة من IR نحو [0;1] بما يلي F(x)=p(X< x)
لدينا : X(Ω)={0;1;2;3;4}

x∈]-∞;0]	F(x)=0
x∈]0;1]	F(x)=p(X=0)=0,2
x∈]1;2]	F(x)=p(X=0)+p(X=1)=0,3
x∈]2;3]	F(x)=p(X=0) +p(X=1) +pX=2)=0,7
x∈]3;4]	F(x)=p(X=0) + p(X=1) +p(X=2)+p(X=3)=0,9
x∈]4;+∞[	F(x)=1

2) المنحنى (C_F)