1- Ensemble et partie d'un ensemble

1.1 Ensemble

1.1.1 Définition

Un ensemble est un objet qui collecte des éléments s'ils existent.
Un ensemble est noté par une lettre E ou F ou G ..

1.1.2 Notations

1) L'ensemble qui ne contient aucun élément est appelé ensemble vide, noté ∅.
2) Soit x un élément d'un ensemble E.
On écrit x∈E et on lit x appartient à E.
3) On écrit x∉E si x n'appartient pas à E.

Exemples
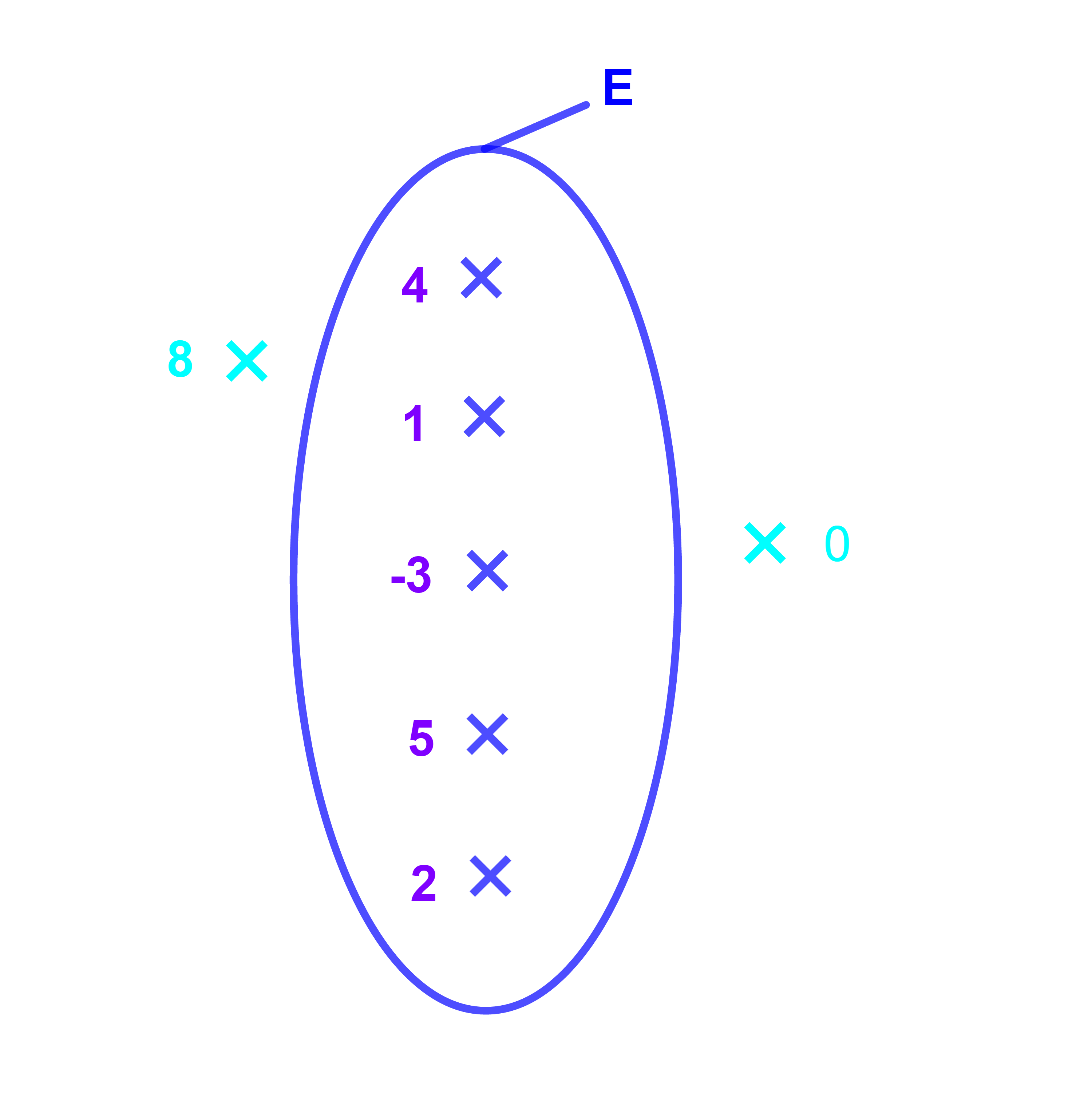
On considère l'ensemble E={-3;1;2;4;5}.
Le nombre 2 est un élément de E donc 2∈E.
5 est un élément de E donc 5∈E.
0 n'est pas un élément de E donc 0∉E.

1.2 Ensemble par extention

1.2.1 Définition

Un ensemble en extension est une liste des éléments.

1.2.2 Exemple

E={-3;1;2;4;5}.
F={0 ; 5 ; 14}.
G={8}.

1.3 Ensemble par compréhension

1.3.1 Définition

Un ensemble en compréhension est un ensemble définie par une propriété.

1.3.2 Exemples

1) E={x∈IN/ 0<x<10 et x impair} est une écriture en compréhension
et E={1;3;5;7;9} son écriture en extension.
2) F={x∈ℤ/ |x|≤4} est une écriture en compréhension
et F={-4;-3;-2;-1;0;1;2;3;4} son écriture en extension.

Exercice 1 tp

Ecrire les ensembles suivants en extension
A=IN∩[-2;√(30)].
B={x∈ℤ/ x|20}.
C={x∈IN/x+4|x+19}.

Exercice 2 tp

Ecrire les ensembles suivants en compréhension
E={1;3;5;7;9;11;13;15}.
F={0;7;14;21;28;25;42;49}.
G={1;2;4;5;8;10}.

1.4 Partie d’un ensemble

1.4.1 Exemples

On considère l'ensemble ℤ.
Tous les entiers naturels appartiennent à ℤ.
On dit que l'ensemble IN est une partie de ℤ.
On écrit donc IN⊂ℤ et on lit IN est inclu dans ℤ.

1.4.2 Définition

Soient E et F deux ensembles non vides.
On dit que F est une partie de E et on écrit F⊂E si tout élément de F est un élément de E.

En d'autre terme
F⊂E ⇔ (∀x∈ F): x∈E.

Exercie 3 tp

Soit E={x∈ℤ/ x|20}.
1) Déterminer une partie de E constituée de nombres impairs.
2) Déterminer une partie de E constituée de nombres divisibles par 5.