1.3 نهاية مقلوب دوال اعتيادية عند +∞ و -∞

1.3.1 نشاط

اتمم الجدول واستنتج

x		-∞	-104	10³	105	..	+∞
1		..	..	..	..	..	..
x
1		..	..	..	..	..	..
x²
1		..	..	..	..	..	..
x³

1.3.2 نتيجة 1

عندما تكبر قيمة x فان العددين

1	و	1
x²		x

يصغران ويقتربان من 0 نكتب اذن

lim +∞	1	= 0	lim +∞	1	= 0
	x			x²

n∈IN*			lim +∞	1	= 0
				xn

1.3.3 نتيجة 2

عندما تصغر قيمة x وتقترب من -∞ فان العددين

1	و	1
x²		x

يقتربان من 0 نكتب اذن

lim -∞	1	= 0		lim -∞	1	= 0
	x				x²

(n∈IN* )	lim -∞	1	= 0
		xn

أمثلة

lim -∞	1	= 0
	x5
lim -∞	1	= 0
	x4

1.4 نهاية مقلوب الدالتين x→x² و x→xⁿ عند 0 حيث n زوجي

1.4.1 خاصيات

ليكن n عددا طبيعيا زوجيا غير منعدما

lim 0	1	= +∞
	x²
lim 0	1	= +∞
	xn

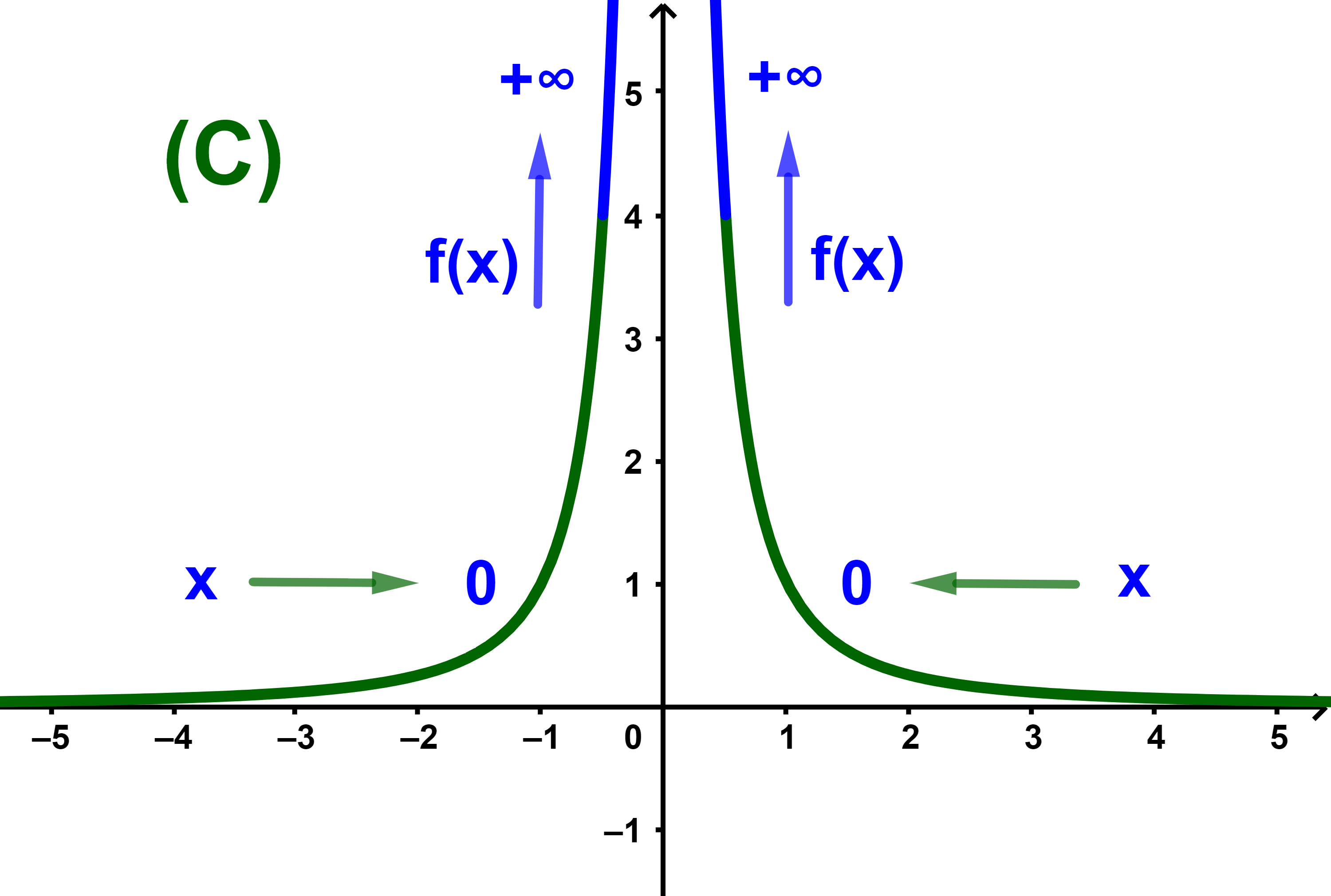
1.4.2 مثال

lim 0	1	= +∞		lim 0	1	= +∞
	x4				x8

تمرين 1 tp

لتكن f دالة عددية معرفة بما يلي

f(x) =	1	+ 2
	x²

احسب النهاية التالية

lim 0

f(x)

تصحيح

لدينا

lim 0	f(x) - 2 =	lim 0	1	= +∞
			x²

اذن

lim 0

f(x) = +∞