Rappel
Branches infinies 1) Soient f une fonction numérique de la variable réel x et (C) sa courbe représentative dans un repère orthonormé
(O;i^→;j^→)
Si l'une des coordonnées d'un point M(x ; y) de la courbe (C) tend vers ∞ alors la courbe admet une branche infinie
(c'est à dire x→±∞ ou f(x)→±∞).

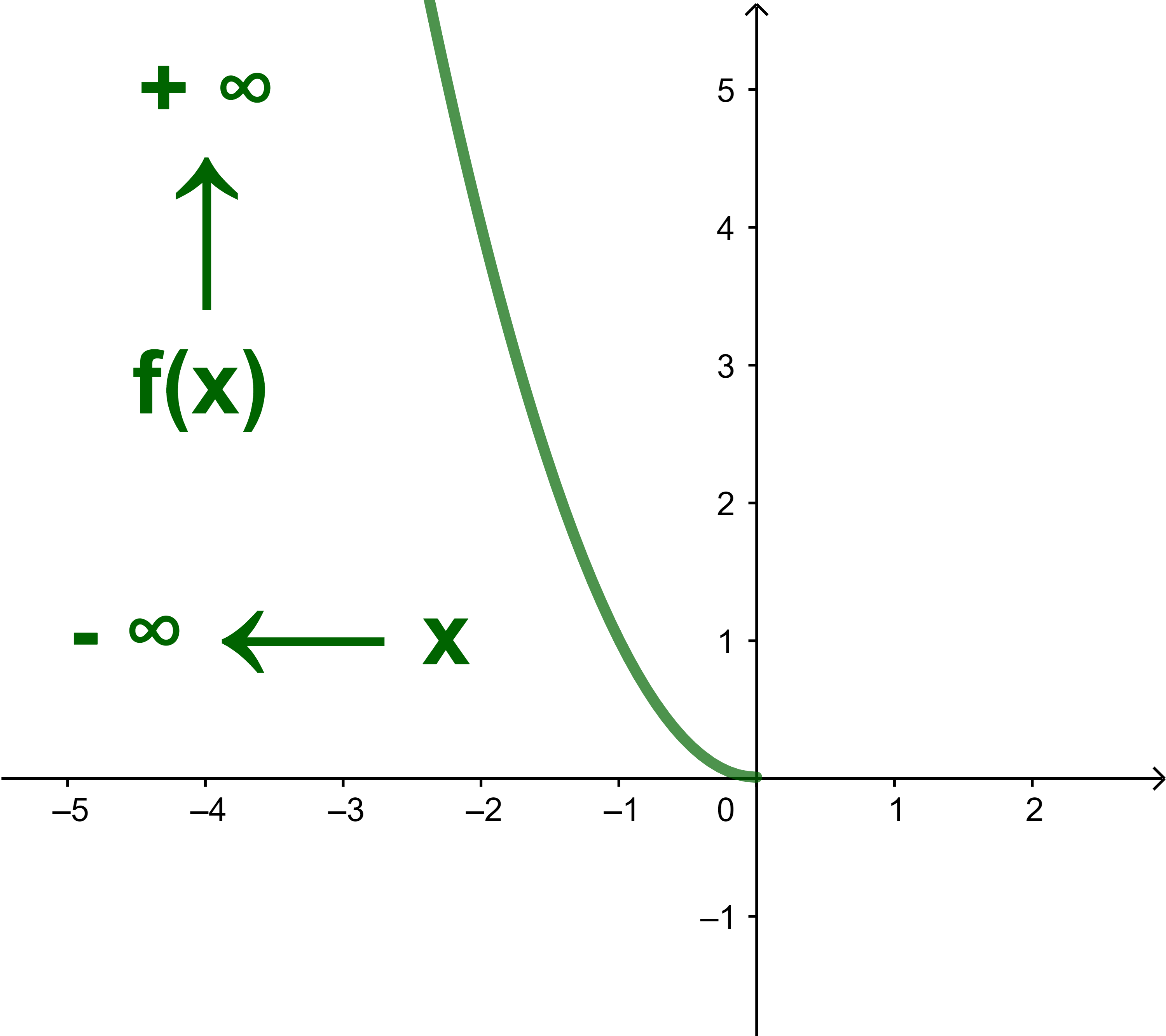
Cas (x→-∞ et f(x)→+∞)

Cas (y→ - ∞ avec y=f(x))

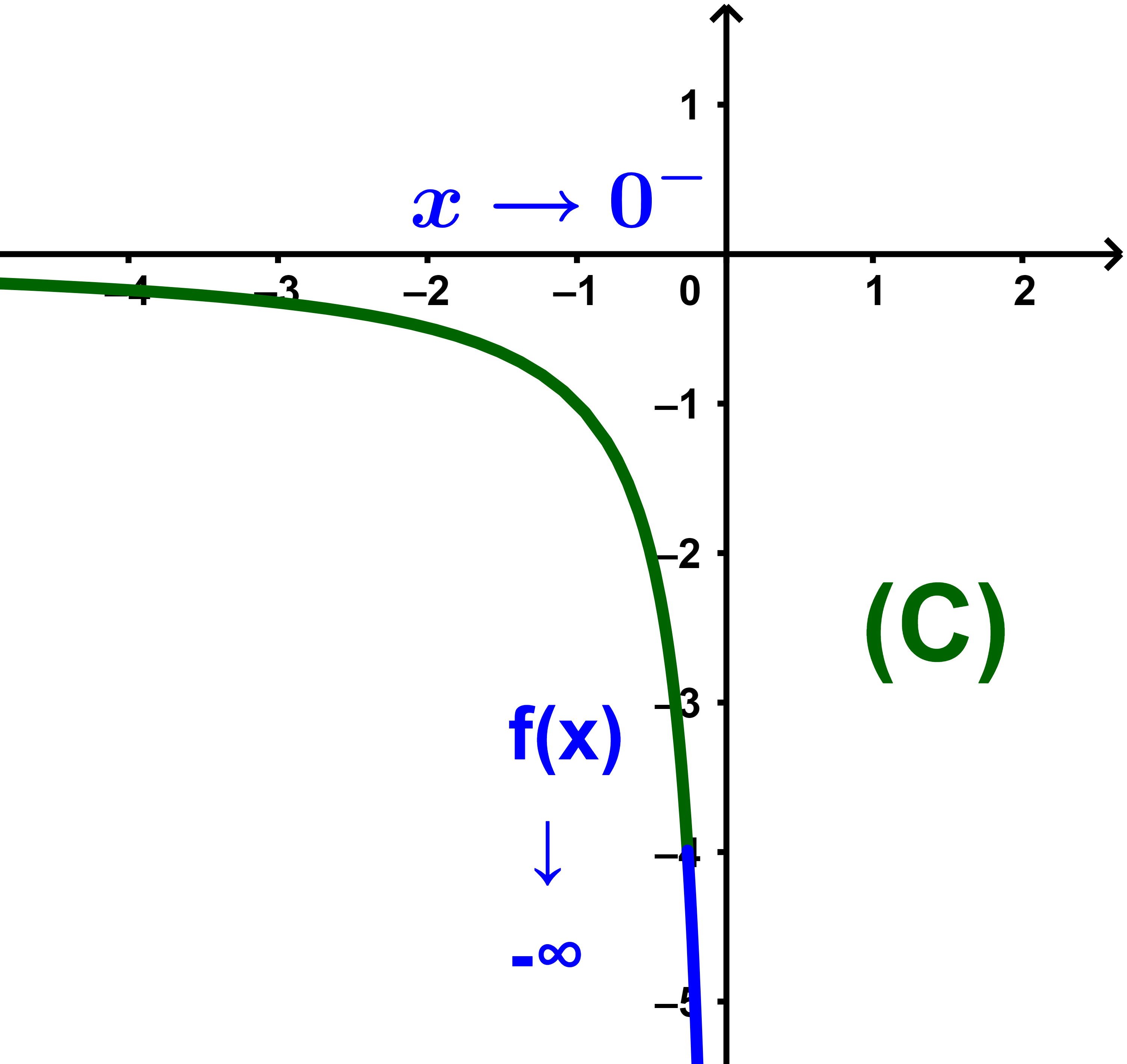
2) La droite d'équation x = a est asymptote à (C) Si l'une des conditions suivantes est vérifiée

lim a-	f(x) = +∞		lim a-	f(x) = -∞
lim a+	f(x) = +∞		lim a+	f(x) = -∞

3) La droite d'équation y = b est asymptote à (C) au voisinage de - ∞

Si

lim -∞

f(x) = b

4) La droite d'équation y = b est asymptote à (C) au voisinage de + ∞

Si

lim + ∞

f(x) = b