Exercice 1 tp

Soient E; F et G trois ensembles définis par le diagramme suivant

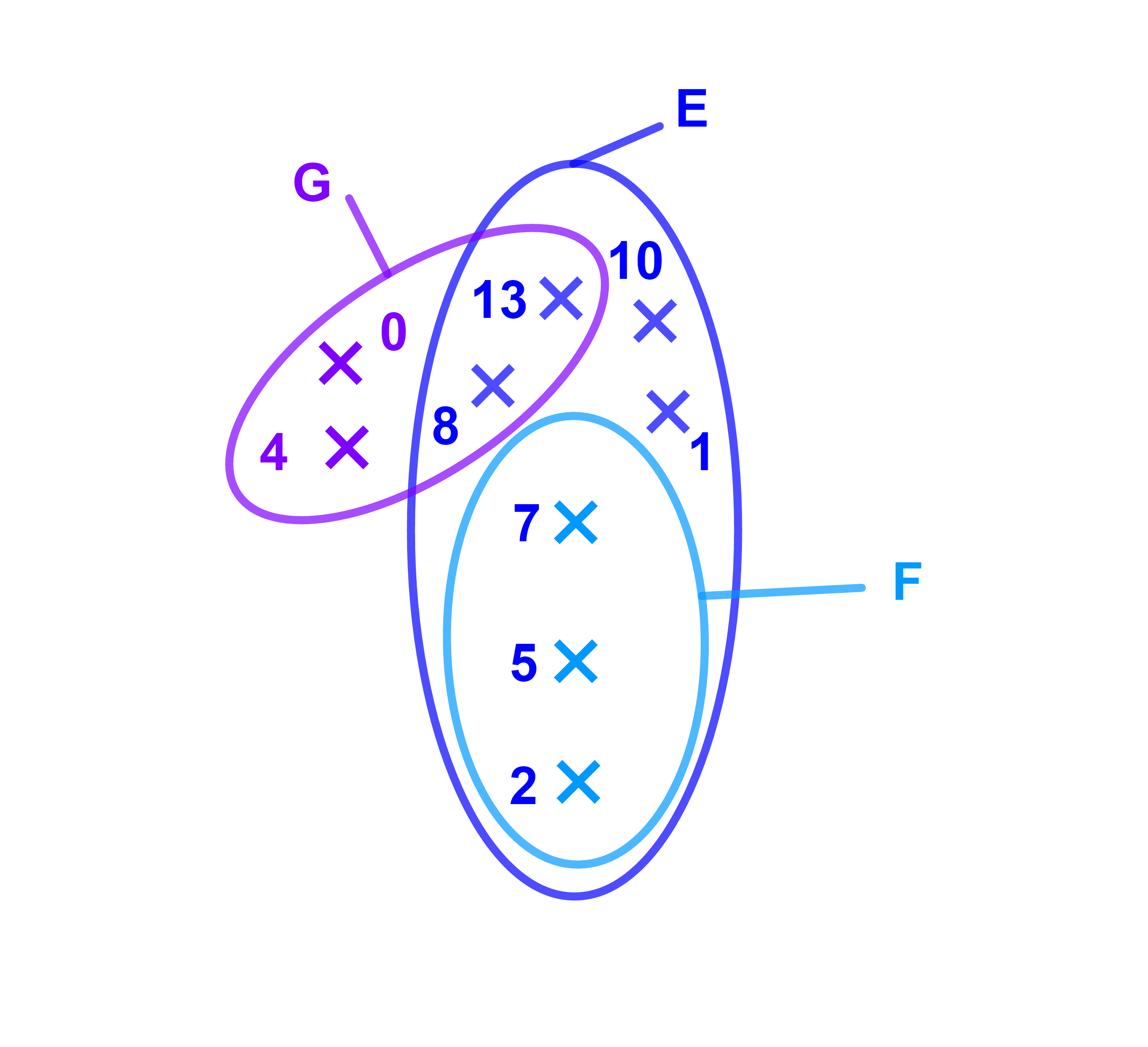
Déterminer E∪F; E∪G ; E∩G et F∩G.

Exrcice 2 tp

Une personne a 3 chemises; 4 pantalons et 2 paires de chaussures
Quel est le nombre de tenues différentes pour cette personne ?

Correction

Elle a 3 possibilités d'habiller une chemise; 4 possibilités d'habiller un pantalon et 2 possibilités d'habiller une paire de chaussures
d'après le Principe fondamental du dénombrement, le nombre de tenues différentes est 3×4×2=24.

Exercice 3 tp

Déterminer le nombre de résultats possibles de la course de 100 mètres, à laquelle participent 8 coureurs.

Correction

Il s'agit des permutations donc Le nombre de résultats possibles de la course de 100 mètres est 8!=40320.

Exercice 4 tp

Une urne contient 7 boules numérotées par 0 ; 2 ; 4 ; 13 ; 14 ; 17 ; 18 . On tire une boule de l'urne
0 2 4 13 14 17 18

Quel est le nombre de possibilités de tirer une boule portant un nombre pair ?

Correction

Les boules numérotérs en nombre pair 0 2 4 14 18 Il y a donc cinq résultats

Exercice 5 tp

Une urne contient 5 boules bleues et deux boules vertes, toutes les boules sont indiscernables au toucher,
on tire au hasard deux boules successivement et avec remise
1) Calculer cardΩ
2) Calculer le nombres d'éventualités de chacun des événements suivants
B: tirer deux boules bleues
V: tirer deux boules vertes

M: tirer deux boules de même couleur
D: tirer deux boules de couleurs différentes

Correction

dans cette expérience, l'ordre est important mais avec répétition, il s'agit donc des arrangements avec répétitions
1) cardΩ = 7x7 = 49

2) L'événement B: tirer 2 boules bleues
cardB = 5×5 = 25
L'événement V: tirer 2 boules vertes
cardV = 2x2 = 4
L'événement M: tirer 2 boules bleues ou 2 boules vertes, l'union de deux événements incompatibles donc M=B∪V , or B∩V=∅
alors cardM = 5²+2² = 29
L'événement N: tirer (1 boule bleue et 1 boule verte) ou (1 boule verte et 1 boule bleue)
donc cardN = 5x2+2x5 = 20.