(1) الاشتقاق
للتذكير
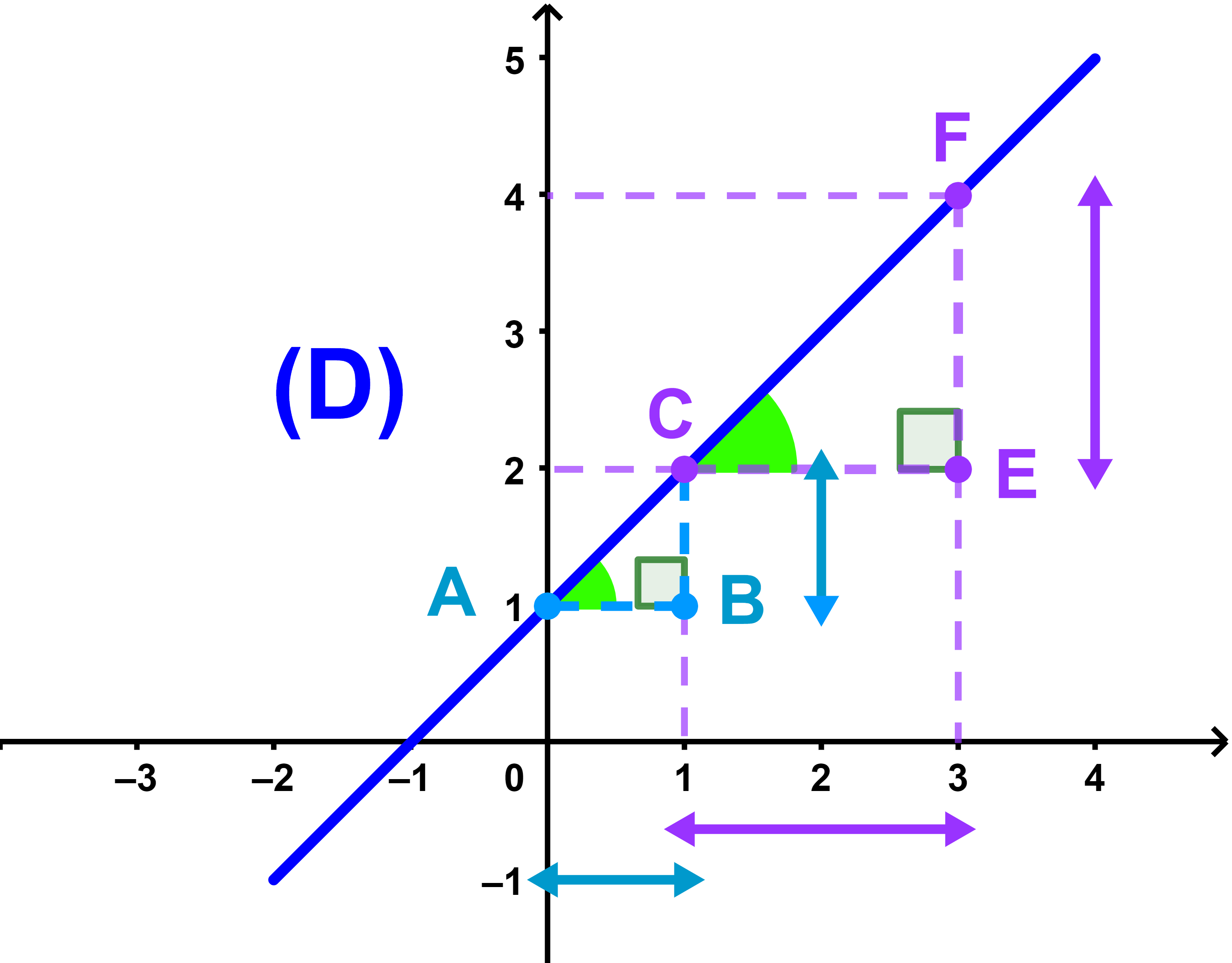
الميل
لتكن A و C نقطتين مختلفتين من مستقيم (D)
النسبة التالية
| m = | yC - yA |
| xC - xA |
هي ميل أو المعامل الموجه للمستقيم (D)
والمعادلة المختصرة للمستقيم (D) كتب على الشكل
y = mx + p حيث p هو الارتوب عند الأصل
العدد المشتق ومعادلة المماس
لتكن f دالة عددية معرفة على مجال I و a∈I
و (C) منحناها في معلم متعامد ممنظم
(O ; i→ ; j→)
نقول ان الدالة f قابلة للاشتقاق في نقطة a يعني يوجد عدد حقيقي L بحيث
lim x→a |
f(x) - f(a) | = L | |
| x-a |
العدد L يسمة العدد المشتق للدالة f في النقطة a ونرمز له ب f '(a)
lim x→a |
f(x) - f(a) | = f '(a) | |
| x-a |
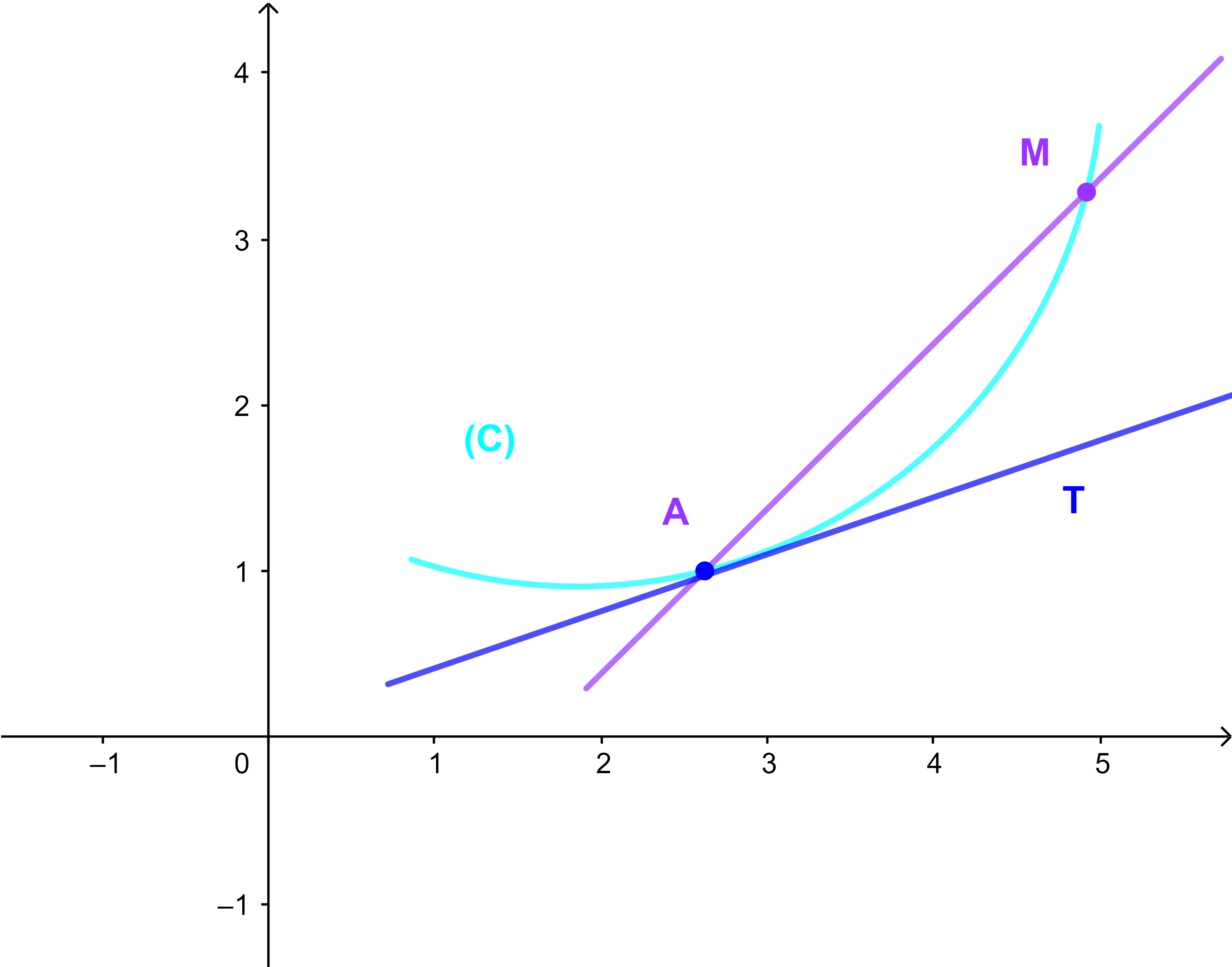
والمنحنى (C) يقبل مماسا (T) في النقطة ذات الأفصول a
ميله العدد المشتق f '(a) ومعادلة المماس (T)
تكتب على الشكل y = f '(a)(x - a) + f(a)
العمليات على الاشتقاق
1) لتكن f و g دالتين قابلتين للاشتقاق على مجال I و n∈IN*
الدوال f + g و k.f و f×g و f n هي ايضا دوال قابلة للاشتقاق على المجال I ولدينا لكل x∈I
| (f + g) '(x) | = | f '(x) + g '(x) |
| (k.f) '(x) | = | k.f '(x) |
| (f g) '(x) | = | f '(x)g(x) + f(x)g '(x) |
| (fn) '(x) | = | nfn-1(x)f '(x) |
(∀x∈IR): (xn)' = nxn-1
ملاحظة الدوال الحدودية قابلة للاشتقاق على IR
2) لتكن f و g دالتين قابلتين للاشتقاق على مجال I
اذا كانت الدالة g لا تنعدم على I فان مقلول g قابل للاشتقاق على I ولكل x∈I
| ( | 1 | )'(x)= | - g '(x) |
|---|---|---|---|
| g | (g(x))² |
بالاضافة الى ذلك فان خارج f على g قابل للاشتقاق ايضا على I ولكل x∈I
| ∀x∈I; ( | f | )'(x) = | f'(x)g(x) - f(x)g'(x) |
|---|---|---|---|
| g | (g(x))² |
ملاحظة الدوال الجذرية قابلة للاشتقاق على مجموعة تعريفها
الرتابة
1) لتكن f دالة قابلة للاشتقاق على مجال I
f تزايدية على I ⇔ (∀x∈I) f '(x) ≥ 0
f تناقصية على I ⇔ (∀x∈I) f '(x) ≤ 0
f تابتة على I ⇔ (∀x∈I) f '(x) = 0
2) لتكن f دالة قابلة للاشتقاق على مجال I
f تزايدية قطعا على I ⇔ (∀x∈I) f '(x) > 0
f تناقصية قطعا على I ⇔ (∀x∈I) f '(x) < 0
المطراف
1) لتكن f دالة عددية معرفة على مجال I و a∈I
نقول ان f(a) مطراف للدالة f على I اذا كان قيمة قصوى او قيمة دنيا للدالة f على المجال I
2) لتكن f دالة قابلة للاشتقاق على I و a∈I
اذا كانت f تقبل مطرافا عند a فان f '(a)=0
3) لتكن f دالة قابلة للاشتقاق على مجال I و a∈I
اذا كانت f ' تنعدم في a وتتغير اشارتها بجوار a فان f(a) مطراف للدالة f